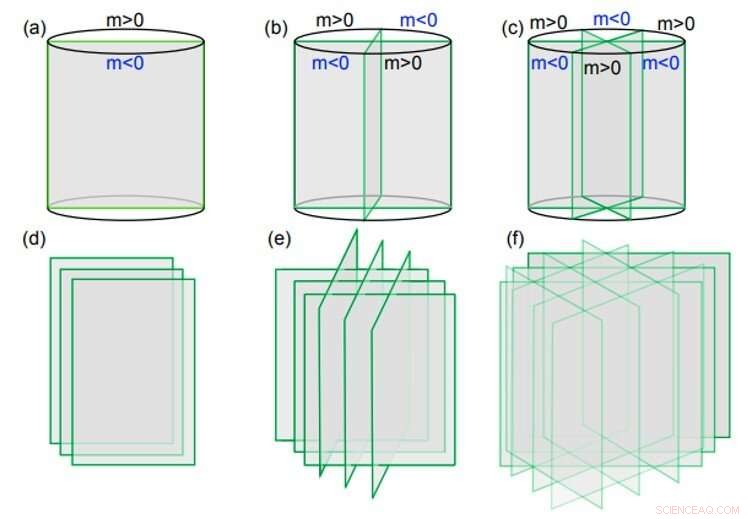
Construções de espaço real para C2, 4, 6-rotação e simetrias de reversão de tempo. (a-c) mostram na ausência de simetrias de translação, as construções mínimas de dupla, simetria de rotação quádrupla e seis vezes protegida estados topológicos em três dimensões, onde cada plano é um estado topológico protegido por simetria interna bidimensional de bósons ou férmions. Se for um isolante topológico bidimensional, os estados resultantes são os isoladores cristalinos topológicos estudados no texto. (d-f) são extensões simples das construções mínimas, construção de modelos tridimensionais com simetrias de translação. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374.
Em um novo relatório sobre Avanços da Ciência , Chen Fang e Liang Fu, do Laboratório Nacional de Física da Matéria Condensada de Pequim, na China, Instituto Kavli de Ciências Teóricas e Departamento de Física, Instituto de Tecnologia de Massachusetts nos EUA. Detalhou a descoberta de novos tipos de anomalias quânticas em sistemas bidimensionais com simetria de reversão de tempo (T) (conservação de entropia) e simetria de rotação discreta; onde uma forma retém a mesma estrutura após a rotação por uma volta parcial e ordem. Eles então perceberam fisicamente estados anômalos na superfície de novas classes de isoladores cristalinos topológicos (TCIs) normais ao eixo de rotação e suportando um modo helicoidal. A presença de modos helicoidais permitiu-lhes formar um novo dispositivo quântico a partir de um isolador cristalino topológico conhecido como nanorod helicoidal com condutância longitudinal quantizada.
Um único sabor de férmion relativístico sem massa (partículas elementares) pode ter anomalias quânticas onde a conservação da corrente de simetria global é quebrada no nível quântico. Exemplos bem conhecidos incluem a anomalia quiral de férmions de Weyl em três dimensões (3-D), e anomalia de paridade em 2-D. No presente trabalho, Fang e Fu apresentaram uma nova anomalia quântica associada com inversão de tempo (T) e simetria rotacional discreta (C n =2, 4, 6). Essas anomalias só poderiam existir em teorias que quebrassem as simetrias de rotação contínua em 2-D. Materiais específicos como TCIs (isoladores cristalinos topológicos) podem hospedar estados de superfície robustos que têm uma dispersão de Dirac (semelhante ao grafeno) em relação a portadores sem massa. Romper a simetria protetora dentro de tais materiais pode fazer com que os portadores adquiram massa.
Formando novas classes de TCIs
Em TCIs, a topologia e a simetria do cristal se entrelaçam para formar estados de superfície com características distintas. A quebra da simetria do cristal em TCIs pode conferir massa a férmions Dirac sem massa; Portanto, a presença de estados de superfície topológicos protegidos por simetrias de cristal é uma propriedade definidora dos TCIs. Os 230 grupos espaciais previamente identificados que descrevem todas as simetrias de cristal possíveis permitem muitas classes diferentes de TCIs. Os pesquisadores haviam encontrado anteriormente uma classe de TCI protegida por simetria de reflexão em semicondutores IV-VI e outra classe de TCI protegida conjuntamente por reflexão de deslizamento e simetria de reversão de tempo dentro de isoladores de grande espaço para formar férmions experimentais de "ampulheta", enquanto teoriza várias outras classes de TCIs.

O esquema dos estados sem intervalos em duas dimensões que têm simetrias de rotação e reversão no tempo. Existem (A) dois, (B) quatro, e (C) seis cones de Dirac, relacionados um com o outro por dois-, quatro-, e simetrias de rotação de seis vezes, respectivamente, na primeira zona de Brillouin. Os contornos são os limites das zonas invariantes de Brillouin, ao longo da qual a fase de Berry é quantizada em zero ou π. Crédito:avanços da ciência, doi:10.1126 / sciadv.aat2374.
O procedimento de pesquisa padrão para encontrar materiais topológicos envolve a computação da estrutura de banda de um determinado material para compreender os estados eletrônicos, em seguida, forneça essas informações a uma fórmula para revelar se o material é topológico. Além disso, a estrutura da banda eletrônica, conhecido como a relação entre a energia de um elétron e seu quase-momento, pode determinar se um material é um metal ou isolante. Os pesquisadores recentemente provaram uma teoria para prever e descobrir experimentalmente esses materiais topológicos. No presente trabalho, Portanto, Fang et al. previu uma nova classe de TCIs protegidos conjuntamente por rotação n-dobra e simetria de reversão de tempo para exibir estados de superfície topológicos contendo cones de Dirac sem massa nas superfícies superior e inferior.
Compreendendo a anomalia rotacional
O estudo da anomalia levou-os a teorizar novas classes de invariantes de reversão no tempo (onde as leis subjacentes não são sensíveis à direção do tempo) TCIs com C n =2, 4, 6 simetria de rotação. Esses TCIs tinham estados de superfície anômalos nas superfícies superior e inferior. Para cada nova classe de TCIs, a equipe construiu o invariante topológico correspondente em relação às funções de onda de Bloch no espaço de momento. Com base na redução dimensional (número de variáveis aleatórias ou atributos em consideração) e estados de parede de domínio (estruturas magnéticas de largura finita que separam regiões de magnetização uniforme dentro de um material magnético), os cientistas forneceram ainda uma compreensão unificada do espaço real desses TCIs. Eles previram vários materiais para realizar os estados de superfície anômalos protegidos por simetrias de rotação dupla e quádrupla. Os pesquisadores então propuseram um novo dispositivo quântico baseado nas anomalias, conhecido como a "haste helicoidal, "feito usando esses novos TCIs.
Duas estruturas distintas de pseudospin com preservação de C2. A estrutura pseudopin ao longo do contorno de energia igual para algum E> 0, nos hamiltonianos efetivos (A) h + (kx, ky) =kxσx + kyσy e (B) h− (kx, ky) =kxσx - kyσy. Vê-se que a estrutura da esquerda possui simetria de rotação contínua e a da direita não; também é visto que a estrutura certa ainda preserva a rotação dupla. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374. 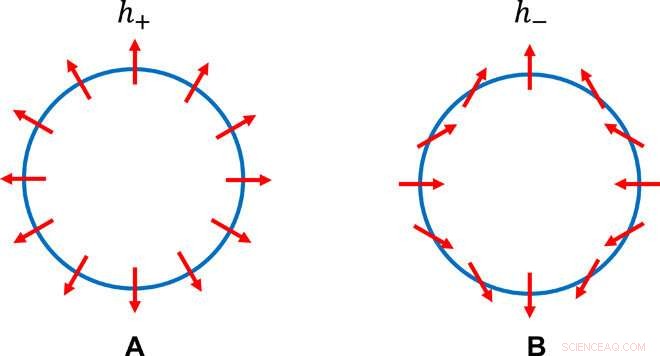
Para construir os novos TCIs e formar a topologia no espaço de momento, Fang et al. poderia adicionar dois invariantes de reversão no tempo (simetria T), isoladores topológicos fortes (TIs), cada um com simetria rotacional n vezes. Eles consideraram a hibridização permitida por simetria entre os férmions de Dirac de superfície para TIs para obter os estados de superfície desejados de TCIs. Os pesquisadores descreveram os férmions de Dirac usando h + e h - texturas de spin semelhantes a vórtices em espaço de impulso com quiralidade para destros e esquerdos. Os pesquisadores observaram a presença e ausência de simetria de rotação contínua, olhando para o padrão de vetor pseudospin em alguns contornos de energia igual de h + e h - respectivamente.
Depois de estabelecer a estrutura de banda do estado de superfície TI, Fang et al. forneceu uma explicação alternativa de sua natureza topológica da perspectiva do espaço real, semelhante a uma abordagem de pesquisa anterior. A abordagem do espaço real adicionou perturbações permitidas pela simetria para quebrar a simetria translacional e separar os férmions de Dirac sem massa na superfície para um estudo mais aprofundado. Os fenômenos facilitaram estados TCI não triviais e demonstrações de sua robustez sob interações eletrônicas. Por esta, eles consideraram um modelo de duplo TI de um TCI colocado dentro de um cilindro de um tamanho maior do que o comprimento de correlação e a superfície, suave na escala atômica. Para C 4, 6 -TCI colocado em um cilindro, as localizações dos modos nos estados de superfície não foram fixados em nenhuma dobradiça física ou interseção de superfícies cristalinas. Embora a forma cilíndrica contivesse simetria de rotação contínua, o sistema descrito no estudo o decompôs em simetria rotacional discreta, para indicar a existência de linhas 1-D sem intervalos, mesmo em um cilindro liso perfeitamente em escala atômica.
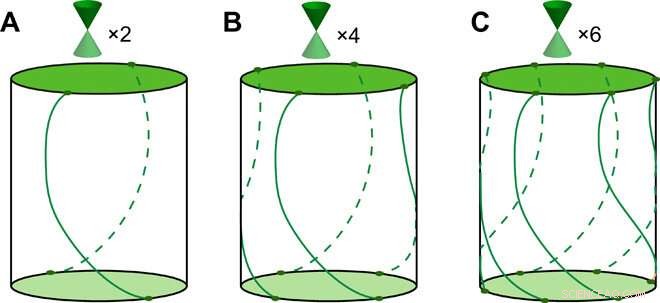
Estados de superfície de rotação TCI. Esquemas dos estados de superfície nas superfícies superior e inferior e os estados de borda nas superfícies laterais com espaçamento dos novos TCIs protegidos por (A) duplo, (B) quádruplo, e (C) simetrias de rotação de seis vezes na geometria da haste. As superfícies superior e inferior têm cones de Dirac, e na superfície lateral, dois, quatro, e seis modos de borda helicoidal conectam as duas superfícies; eles podem ter forma e posição arbitrárias, mas estão relacionados entre si por dois -, quatro-, e rotações de seis vezes, respectivamente. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374.
Fang et al. então observou a possibilidade de compreender estados cristalinos topológicos a partir de uma perspectiva de redução dimensional, onde o estado 3-D pode ser considerado como um conjunto de camadas desacopladas de estados topológicos 2-D. Todos os três tipos de novos TCIs introduzidos neste trabalho podem, portanto, ser construídos a partir de TIs 2-D. Fang et al. usaram esta construção para estender sua teoria de estados topológicos protegidos por simetria de forte interação protegidos por simetria de rotação e qualquer simetria local, incluindo, mas não limitado a simetria de reversão de tempo.
Uma vez que os modos helicoidais 1-D são bem conhecidos por serem livres de retroespalhamento devido à simetria de reversão do tempo, esta propriedade única permitiu Fang et al. para projetar um nanorod helicoidal a partir desses novos materiais. Cada modo helicoidal exigia apenas simetria de reversão de tempo para proteção e a simetria de rotação garantiu que os modos n-helicoidais não se cruzassem no espaço real e se separassem. Desta maneira, contanto que a simetria de rotação não fosse consideravelmente quebrada, esses modos de borda helicoidal permaneceriam estáveis, embora eles não se relacionem mais entre si por meio de uma rotação - para formar novas classes de TCIs com anomalia de rotação de superfície.
© 2020 Science X Network