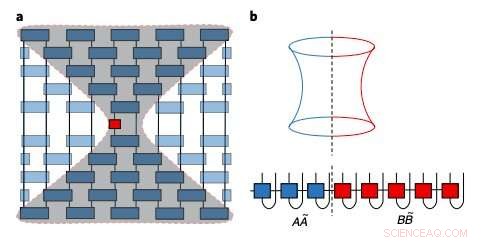
Esboço do cone de luz emergente e estrutura de emaranhamento de operadores locais de Heisenberg em formas de rede de tensores. Crédito:Xu &Swingle.
Na física quântica, embaralhamento é a dispersão de informações quânticas em um sistema quântico complexo, como sistemas quânticos caóticos de muitos corpos. Este processo pode tornar as informações quânticas difíceis ou impossíveis de acessar, particularmente ao usar métodos de física simples e convencionais.
O embaralhamento pode ser medido usando correlacionadores ordenados fora do tempo (OTOCs), que são medidas do caos quântico vinculado ao crescimento dos operadores de Heisenberg. Pesquisadores da Universidade de Maryland introduziram recentemente um novo método para calcular OTOCs de operadores locais em sistemas 1-D. Este método, apresentado em um artigo publicado em Física da Natureza , poderia, em última análise, ser usado para estudar o embaralhamento em sistemas quânticos complexos.
"A questão básica que estávamos tentando entender é como o caos se espalha no espaço nos sistemas quânticos, "Brian Swingle, um dos pesquisadores que realizou o estudo, disse a Phys.org. "Pense no experimento mental do efeito borboleta - queríamos saber:se uma borboleta bate suas asas, quão rápido essa perturbação se espalha no espaço? Queríamos entender isso especificamente no contexto de sistemas quânticos compostos de muitas partículas. "
Estudos anteriores investigando como o caos se espalha no espaço dentro de sistemas quânticos reuniram várias observações interessantes, pintando uma paisagem interessante, mas bastante complexa de comportamentos possíveis. Muitos desses estudos, Contudo, foram baseados em suposições especiais e isso torna mais difícil determinar até que ponto suas conclusões podem ser generalizadas para outros sistemas.
Em seu estudo, Swingle e seu colega Shenglong Xu começaram a investigar quais comportamentos revelados em estudos anteriores são genéricos para todos os sistemas quânticos. Eles também esperavam entender como se pode pensar sobre a paisagem de possibilidades que ocorrem em diferentes sistemas especiais.
"Para entender qual era o comportamento genérico, precisávamos de um método para calcular OTOCs em sistemas genéricos, "Swingle disse." Tal método precisaria utilizar alguma propriedade genérica de OTOCs em sistemas locais. "
A ideia dos pesquisadores era usar a propriedade do cone de luz de sistemas quânticos, que implica que fora do cone de influência em expansão decorrente da batida de asa da borboleta metafórica, o sistema dificilmente é perturbado. Em outras palavras, fora do 'cone de borboleta', o efeito da borboleta permanece pequeno.
Na mecânica quântica, as ações são representadas como operadores e a pequenez de um determinado efeito se traduz na simplicidade do operador. Aproveitando essa simplicidade, Swingle e Xu foram capazes de representar o operador de uma forma computacionalmente útil (ou seja, como um 'operador de produto de matriz'), a fim de realizar os cálculos necessários para acessar o embaralhamento.
"Existem duas conquistas importantes em nosso estudo, "Swingle disse." Primeiro, planejamos um arcabouço teórico para classificar vários comportamentos possíveis do OTOC. Essa estrutura era geral o suficiente para incluir todos os exemplos conhecidos anteriormente. Segundo, formulamos um método de propósito geral para calcular OTOCs, um método que pode ir além dos cálculos anteriores. "
Swingle e Xu já usaram seu método para calcular OTOCs de operadores locais para estudar uma variedade de sistemas genéricos. Interessantemente, eles descobriram que vários desses sistemas se encaixam em sua estrutura teórica. Em um estudo de acompanhamento apresentado em Revisão Física X , os pesquisadores também usaram seu método para reunir evidências de que OTOCs em sistemas caóticos genéricos têm um comportamento universal.
"Acompanhamos esse trabalho aplicando nossa tecnologia a vários sistemas diferentes que estão sendo estudados em experimentos de mesa em todo o mundo, ", Disse Swingle." Agora também estamos generalizando a abordagem para incluir novos tipos de efeitos, incluindo o estudo de sistemas em baixa temperatura, onde a velocidade de propagação do caos tende a diminuir. "
© 2019 Science X Network