
Os processos de Markov têm sido usados para modelar o acúmulo de pilhas de areia. Crédito:Santa Fe Institute Press
Os cientistas acreditam que o tempo é contínuo, não discreto - falando grosso modo, eles acreditam que não progride em "pedaços, "mas sim" flui, "sem problemas e continuamente. Portanto, eles costumam modelar a dinâmica dos sistemas físicos como processos de Markov de tempo contínuo", "nomeado após o matemático Andrey Markov. Na verdade, cientistas usaram esses processos para investigar uma série de processos do mundo real de dobrar proteínas, aos ecossistemas em evolução, para mudar os mercados financeiros, com sucesso surpreendente.
Contudo, invariavelmente, um cientista só pode observar o estado de um sistema em momentos discretos, separados por alguma lacuna, em vez de continuamente. Por exemplo, um analista do mercado de ações pode observar repetidamente como o estado do mercado no início de um dia está relacionado ao estado do mercado no início do dia seguinte, construir uma distribuição de probabilidade condicional de qual é o estado do segundo dia dado ao estado no primeiro dia.
Em um par de papéis, um aparecendo no desta semana Nature Communications e um que apareceu recentemente no New Journal of Physics , físicos do Santa Fe Institute e do MIT mostraram que, para que essa dinâmica de dois tempos sobre um conjunto de "estados visíveis" surja de um processo de Markov de tempo contínuo, que o processo de Markov deve realmente se desdobrar em um espaço maior, um que inclui estados ocultos além dos visíveis. Eles ainda provam que a evolução entre um par de vezes deve ocorrer em um número finito de "passos de tempo ocultos", subdividindo o intervalo entre esses dois tempos. (Estritamente falando, esta prova se mantém sempre que a evolução do tempo anterior para o posterior é livre de ruído - consulte o papel para obter detalhes técnicos.)
"Estamos dizendo que existem variáveis ocultas em sistemas dinâmicos, implícito nas ferramentas que os cientistas estão usando para estudar tais sistemas, "diz o co-autor David Wolpert (Santa Fe Institute)." Além disso, em um certo sentido muito limitado, estamos dizendo que o tempo continua em passos de tempo discretos, mesmo que o cientista modele o tempo como se ele continuasse continuamente. Os cientistas podem não ter prestado atenção a essas variáveis ocultas e a esses passos de tempo ocultos, mas eles estão lá, tocando uma tecla, papel nos bastidores em muitos dos artigos que os cientistas leram, e quase certamente também em muitos dos artigos que esses cientistas escreveram. "
Além de descobrir estados ocultos e etapas de tempo, os cientistas também descobriram uma compensação entre os dois; quanto mais estados ocultos existem, quanto menor o número mínimo de passos de tempo ocultos necessários. De acordo com o co-autor Artemy Kolchinsky (Santa Fe Institute), "esses resultados demonstram surpreendentemente que os processos de Markov exibem uma espécie de compensação entre o tempo e a memória, que é freqüentemente encontrado no campo matemático separado de análise de algoritmos de computador.
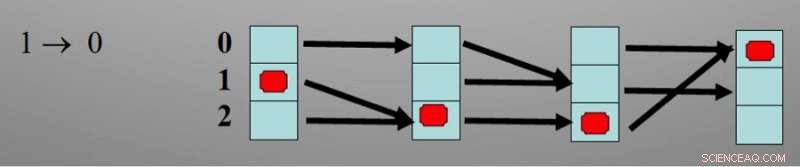
A configuração mínima para inverter um pouco de informação de 1 a 0 requer três estados e três etapas de tempo sequenciais. Crédito:David Wolpert
Para ilustrar o papel desses estados ocultos, o co-autor Jeremy A. Owen (MIT) dá o exemplo de um processo biomolecular, observado em intervalos de uma hora:Se você começar com uma proteína no estado 'a, 'e depois de uma hora geralmente muda para o estado' b, 'e depois de mais uma hora geralmente volta para' a, 'deve haver pelo menos um outro estado' c '- um estado oculto - que está influenciando a dinâmica da proteína. "Está lá em seu processo biomolecular, "ele diz." Se você ainda não viu, você pode ir procurá-lo. "
Os autores tropeçaram na necessidade de estados ocultos e etapas de tempo ocultas enquanto procuravam a maneira mais eficiente em termos de energia para girar um pouco de informação em um computador. Nessa investigação, parte de um esforço maior para entender a termodinâmica da computação, eles descobriram que não há uma maneira direta de implementar um mapa que envie 1 para 0 e também envie 0 para 1. Em vez disso, a fim de inverter um pouco de informação, o bit deve passar por pelo menos um estado oculto, e envolvem pelo menos três etapas de tempo ocultas. (Veja a multimídia em anexo para o diagrama)
Acontece que qualquer sistema biológico ou físico que "calcula" as saídas das entradas, como uma célula de processamento de energia, ou um ecossistema em evolução, ocultaria as mesmas variáveis ocultas do exemplo do bit flip.
"Esses tipos de modelos realmente surgem de uma forma natural, "Owen acrescenta, "com base nas premissas de que o tempo é contínuo, e que o estado em que você está determina para onde você irá a seguir. "
"Uma coisa que foi surpreendente, que torna isso mais geral e mais surpreendente para nós, foi que todos esses resultados se mantêm mesmo sem considerações termodinâmicas, "Wolpert lembra." É um exemplo muito puro do mantra de Phil Anderson 'mais é diferente, 'porque todos esses detalhes de nível inferior [estados ocultos e etapas de tempo ocultos] são invisíveis para os detalhes de nível superior [mapear do estado de entrada visível para o estado de saída visível]. "
"De uma forma muito secundária, é como o limite da velocidade da luz, "Musas Wolpert, "O fato de que os sistemas não podem exceder a velocidade da luz não tem consequências imediatas para a grande maioria dos cientistas. Mas é uma restrição aos processos permitidos que se aplica a todos os lugares e é algo que você sempre deve ter em mente."