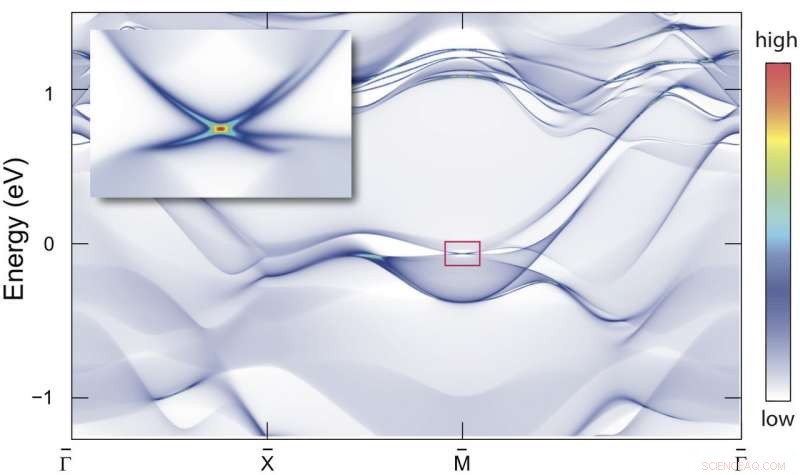
Um material isolante recém-identificado usando os princípios de simetria por trás dos padrões de papel de parede pode fornecer uma base para a computação quântica, de acordo com uma equipe internacional de pesquisadores. Esta amostra de estrôncio-chumbo (Sr2Pb3) tem um estado de superfície de cone de Dirac quádruplo, um conjunto de quatro, estados de superfície eletrônicos bidimensionais que se afastam de um ponto no espaço de momento em linhas retas. Crédito:Benjamin Wieder, Departamento de Física da Universidade de Princeton
Uma equipe internacional de cientistas descobriu um novo, forma exótica de material isolante com uma superfície metálica que poderia permitir uma eletrônica mais eficiente ou até mesmo a computação quântica. Os pesquisadores desenvolveram um novo método para analisar compostos químicos existentes que se baseia em propriedades matemáticas como a simetria que governam os padrões repetidos vistos em papéis de parede do dia a dia.
"A beleza da topologia é que se pode aplicar princípios de simetria para encontrar e categorizar materiais, "disse B. Andrei Bernevig, professor de física em Princeton.
A pesquisa, aparecendo em 20 de julho no jornal Ciência , envolveu uma colaboração entre grupos da Universidade de Princeton, a Universidade da Pensilvânia (Penn), Universidade Sungkyunkwan, Freie Universität Berlin e o Instituto Max Planck de Física da Microestrutura.
A descoberta desta forma de chumbo-estrôncio (Sr 2 Pb 3 ) conclui uma pesquisa de uma década por um material tridimensional indescritível que combina as propriedades eletrônicas exclusivas de grafeno bidimensional e isoladores topológicos tridimensionais, uma fase da matéria descoberta em 2005 em obras independentes de Charles Kane em Penn e Bernevig em Princeton.
Alguns cientistas teorizaram que isoladores topológicos, que isolam em seu interior, mas conduzem eletricidade em sua superfície, poderia servir como base para a computação quântica super-rápida.
"Você pode pensar em um isolante topológico como um beijo de Hershey, "disse Kane, um autor correspondente no artigo. “O chocolate é o isolante e a folha é um condutor. Temos tentado identificar novas classes de materiais em que as simetrias do cristal protegem a superfície condutora. O que fizemos aqui foi identificar o tipo mais simples de isolante cristalino topológico. "
O novo trabalho demonstra como as simetrias de certas superfícies bidimensionais, conhecidos como os 17 grupos de papéis de parede por seus padrões semelhantes aos de papel de parede, restringir o arranjo espacial (topologia) de isoladores tridimensionais.
Em um isolador topológico tridimensional convencional, cada superfície bidimensional exibe um único grupo característico de estados com dispersão em forma de cone. Esses cones se assemelham aos elementos do grafeno chamados cones de Dirac, características que imbuem o material e outros semimetais bidimensionais de Dirac com suas qualidades de transporte eletrônico incomuns, mas são distintos porque o grafeno possui um total de quatro cones Dirac em dois pares que são "colados".
Kane tinha suspeitado que com simetrias de cristal, um segundo tipo de isolante topológico poderia existir com um único par de cones Dirac colados. "O que percebi foi que um único par de cones de Dirac é impossível em um material puramente bidimensional, mas pode ser possível na superfície de um novo tipo de isolante topológico. Mas quando tentei construir tal estado, os dois cones sempre ficavam descolados. "
Uma solução surgiu quando Benjamin Wieder, em seguida, um estudante de graduação no grupo de Kane e agora um associado de pós-doutorado em Princeton, visitou Princeton. Em Princeton, Bernevig e o colega Zhi Jun Wang tinham acabado de descobrir "isolantes de ampulheta" - isoladores topológicos com padrões estranhos de estados semelhantes a ampulheta interligados - que Wieder reconheceu como se estivessem agindo como se você tivesse embrulhado um cristal tridimensional com um tipo especial de papel de parede padronizado.
"Percebemos que você poderia obter não apenas o isolador de ampulheta, mas também este isolador Dirac especial, encontrando um cristal que parecia estar coberto com o papel de parede certo, "disse Wieder.
Em particular, eles reconheceram que um par de cones de Dirac colados pode ser estabilizado em superfícies de cristal que têm duas linhas de intersecção ao longo das quais as superfícies parecem idênticas após serem viradas e viradas perpendicularmente. Essas linhas, conhecido como reflexos de deslizamento, caracterizam os chamados grupos de papéis de parede não simórficos, e, assim, fornecer o nome desta nova fase, que a equipe apelidou de "isolante Dirac não sinmórfico".
Os pesquisadores rapidamente começaram a trabalhar aplicando rigor matemático à inspiração de Wieder, resultando em um novo, metodologia baseada em simetria de papel de parede para diagnosticar a topologia em massa de cristais tridimensionais.
"Os princípios básicos são simples o suficiente para que os esboçamos em guardanapos naquela mesma noite, "disse o co-autor Barry Bradlyn, pesquisador associado do Princeton Center for Theoretical Science (PCTS).
"Mas eles são robustos o suficiente para prever e compreender um zoológico de novas fases topológicas em materiais reais, "disse Wang, um associado de pesquisa de pós-doutorado em física.
A descoberta permitiu aos cientistas relacionar diretamente a simetria de uma superfície à presença de estados topológicos de superfície desejados pela primeira vez, disse Andrew Rappe de Penn, outro co-autor do artigo. "Isso permite um meio elegante e imediatamente útil de projetar os estados desejáveis da superfície e da interface."
Para identificar a fase isolante de Dirac na natureza, os pesquisadores calcularam as estruturas eletrônicas de centenas de compostos previamente sintetizados com superfícies com duas linhas de deslizamento (grupos de papel de parede pgg e p4g) antes de identificar a nova topologia em chumbo-estrôncio.
Os químicos computacionais "sabiam que estavam procurando uma agulha em um palheiro, mas ninguém se preocupou em dizer a eles o quão pequena a agulha pode ser, "disse Jennifer Cano, pesquisador associado da PCTS.
Conforme ainda mais isolantes topológicos exóticos são descobertos, o papel da simetria do grupo de papel de parede, e do especial, cones semelhantes ao grafeno no isolador Dirac, foram ainda mais solidificados.
"Quando você pode dividir um cone de Dirac de superfície real enquanto mantém a simetria de reversão do tempo, algo realmente especial acontece, ", disse Bernevig." Você tem isoladores tridimensionais cujas superfícies bidimensionais também são uma espécie de isolante topológico. "Tais fases foram previstas recentemente em cristais de bismuto e ditelureto de molibdênio (MoTe2) por vários membros da colaboração.
Além disso, com o uso de uma nova teoria, química quântica topológica, os pesquisadores esperam encontrar muito mais dessas fases exóticas.
"Se pudéssemos pintar esses materiais com o papel de parede certo, veríamos mais isoladores Dirac, "disse Wieder, "mas às vezes, o papel de parede errado também é interessante. "