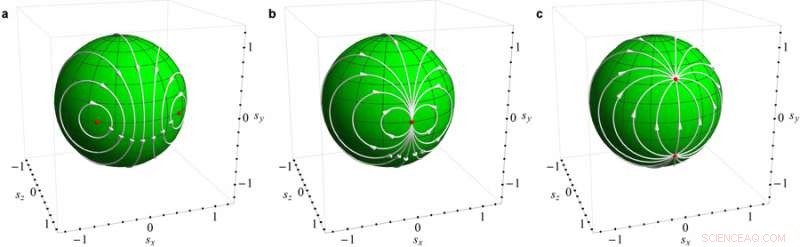
Dois físicos de Argonne ofereceram uma maneira de descrever matematicamente um determinado fenômeno físico chamado de transição de fase em um sistema fora de equilíbrio (ou seja, com energia se movendo através dele) usando números imaginários. A ilustração relaciona a transição de fase à mudança entre as transformações matemáticas de Mobius (a, b, e C). A teoria da física fora de equilíbrio é um objetivo há muito procurado no campo, e poderia nos ajudar a projetar eletrônicos melhores. Crédito:Laboratório Nacional Vinokur / Galda / Argonne
Os números imaginários são uma solução para um problema muito real em um estudo publicado hoje em Relatórios Científicos .
Dois físicos do Laboratório Nacional de Argonne do Departamento de Energia dos EUA ofereceram uma maneira de descrever matematicamente um fenômeno físico específico chamado de transição de fase em um sistema fora de equilíbrio. Esses fenômenos são centrais na física, e entender como eles ocorrem tem sido um objetivo antigo e incômodo; seu comportamento e efeitos relacionados são essenciais para desbloquear possibilidades para novos eletrônicos e outras tecnologias de próxima geração.
Na física, "equilíbrio" se refere a um estado em que um objeto não está em movimento e não tem energia fluindo por ele. Como você pode esperar, a maior parte de nossas vidas ocorre fora desse estado:estamos constantemente nos movendo e fazendo com que outras coisas se movam.
"Uma tempestade, este ventilador rotativo, esses sistemas estão todos fora de equilíbrio, "disse o co-autor do estudo Valerii Vinokur, um Argonne Distinguished Fellow e membro do Instituto de Computação da Argonne-University of Chicago. "Quando um sistema está em equilíbrio, sabemos que está sempre em sua configuração de energia mais baixa possível, mas para o não equilíbrio, este princípio fundamental não funciona; e nossa capacidade de descrever a física de tais sistemas é muito limitada. "
Ele e o coautor Alexey Galda, um cientista com Argonne e o Instituto James Franck da Universidade de Chicago, vinha trabalhando em maneiras de descrever esses sistemas, particularmente aqueles que estão passando por uma transição de fase - como o momento durante uma tempestade quando a diferença de carga entre a nuvem e o solo fica muito alta, e um raio ocorre.
Eles encontraram sua nova abordagem para a física de não equilíbrio em um novo ramo da mecânica quântica. Na linguagem da mecânica quântica, a energia de um sistema é representada pelo que é chamado de operador hamiltoniano. Tradicionalmente, a mecânica quântica sustentou que o operador para representar o sistema não pode conter números imaginários se isso significasse que a energia não sai como um valor "real" e positivo - porque o sistema realmente existe na realidade. Essa condição é chamada de hermiticidade.
Mas os físicos têm examinado com mais atenção os operadores que violam a hermiticidade usando componentes imaginários, Vinokur disse; vários desses operadores descobertos há alguns anos são agora amplamente usados na óptica quântica.
"Percebemos que esses operadores são uma bela ferramenta matemática para descrever processos fora de equilíbrio, " ele disse.
Para descrever a transição de fase, Galda e Vinokur escreveram o operador hamiltoniano, introduziu uma força aplicada para tirá-lo do equilíbrio, e então eles fizeram a força imaginária.
"Este é um truque ilegal do ponto de vista do bom senso; mas vimos que esta combinação, energia mais força imaginária, descreve perfeitamente matematicamente a dinâmica do sistema com atrito, "Vinokur disse.
Eles aplicaram o truque para descrever outras transições de fase fora de equilíbrio, como uma transição Mott dinâmica e um sistema de rotação, e viu os resultados concordarem com experimentos observados ou simulações.
Em seu último trabalho, eles conectaram sua descrição a uma operação chamada transformação de Möbius, que aparece em um ramo da matemática chamado topologia. "Podemos entender as transições de não equilíbrio agora como transições topológicas no espaço de energia, "Galda disse.
Este pequeno mal quântico precisa ser compreendido mais profundamente, eles disseram, mas é valioso da mesma forma; a teoria descreve áreas básicas da física que são de grande interesse para a tecnologia eletrônica de próxima geração.
"No momento, a conexão com a topologia parece um doce matemático, uma coisa linda que ainda não podemos usar, mas sabemos pela história que se a matemática é elegante o suficiente, logo suas implicações práticas se seguem, "Vinokur disse.