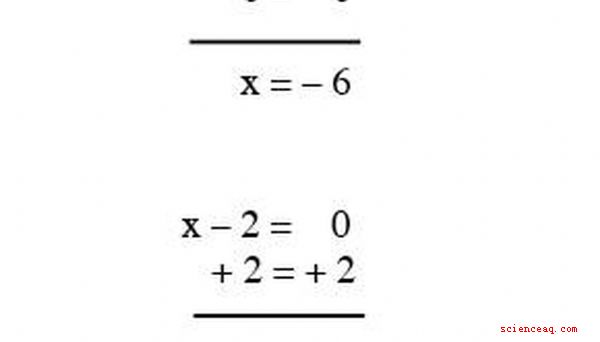
A equação de fatoração é um dos fundamentos da álgebra. Você pode encontrar a resposta para uma equação complexa muito mais fácil, dividindo a equação em duas equações simples. Embora o processo possa parecer desafiador no início, na verdade é bem simples. Você basicamente dividirá a equação em duas unidades, que, quando multiplicadas juntas, criam o item original. Você pode fatorar e resolver equações simplesmente em apenas alguns passos.

Defina sua equação como 0. Digamos que você tenha uma equação como x ^ 2 + 7x = --12, você adicionará 12 a ambas os lados da equação para defini-lo como 0. Uma vez que você fizer isso, sua equação será semelhante a: x ^ 2 + 7x + 12 = 0.

Encontre os fatores. Neste caso, você está agora lidando com x ^ 2 + 7x + 12 = 0. Você encontrará os fatores de 12. Os fatores de 12 incluem 1, 2, 3, 4, 6 e 12.

Certifique-se de que seus fatores se somam à variável do meio. De todos os fatores encontrados no Passo 2, apenas 3 e 4 somam 7, a variável do meio. Certificar-se de que seus fatores se somam à sua variável central é fundamental no fatoramento.

Calcule suas variáveis ​​desconhecidas. Como x é quadrado, quando você fatorar, você terá um x. Veja a próxima seção para saber mais sobre como lidar com variáveis ​​desconhecidas.

Escreva sua nova equação. Como 3 e 4 parecem estar corretos, escreva sua equação como (x + 3) (x + 4) = 0.

Resolva. Agora você pode configurar sua equação para resolver x. Nesta situação, você teria x + 3 = 0 e x + 4 = 0. Ambos mostrariam que x = --3 e x = -4.

Verifique sua equação substituindo seu x com as suas soluções: --3 ^ 2 + 7 (- 3) + 12 = 0 9 + (--21) + 12 = 0 21 + (--21) = 0

- 4 ^ 2 + 7 (- 4) + 12 = 0 16 + (--28) + 12 = 0 28 + (--28) = 0

Defina a equação como 0 e calcule a equação conforme você fiz nas etapas 1 e 2 da última seção se sua equação tem um valor numérico negativo. Por exemplo, você pode receber uma equação como x ^ 2 + 4x - 12 = 0.

Encontre os fatores em x ^ 2 + 4x - 12 = 0. Para esta equação, os fatores são: 1, --1, 2, --2, 3, --3, 4, --4, 6, --6, --12 e 12 para o número 12. Como sua última variável é negativa, seus fatores serão ser positivo e negativo. Nessa situação, 6 e --2 seriam seus fatores, pois quando multiplicados juntos, eles têm um produto de --12 e, quando somados, seu produto é 4. Sua resposta agora será semelhante a (x + 6) ( x - 2) = 0.

Resolva para x como você fez na última seção; x será igual a --6 e 2. Consulte a Figura 1.

Verifique sua equação colocando suas soluções no lugar de x. (--6) ^ 2 + 4 (- 6) - 12 = 0 36 + (--24) - 12 = 0 36 + (--36) = 0

2 ^ 2 + 4 (2) - 12 = 0 4 + 8 - 12 = 0 12 - 12 = 0

Dica

Você também pode seguir estes passos se estiver lidando com uma equação menor, como como x ^ 2 + 5x = 0. Fatore o x, que é comum para ambas as variáveis, e resolva para x. x (x + 5) = 0. x será igual a 0 e --5.