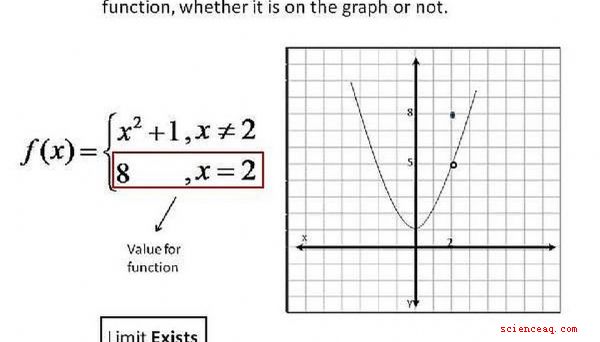
Vamos usar alguns exemplos de funções e seus gráficos para mostrar como podemos determinar se o limite existe quando x se aproxima de um número específico.

Existem quatro maneiras diferentes de determinar se existe um limite por olhando para o gráfico da função. O primeiro, que mostra que o limite existe, é se o gráfico tem um buraco na linha, com um ponto para esse valor de x em um valor diferente de y. Se isso acontecer, o limite existe, embora tenha um valor diferente para a função que o valor do limite. Por favor, clique na imagem para uma melhor compreensão.

Se houver um buraco no gráfico no valor que x está se aproximando, sem nenhum outro ponto para um valor diferente da função, então o limite ainda existe . Por favor, veja o gráfico para uma melhor compreensão.

Se o gráfico tiver uma assíntota vertical, ou seja, duas linhas se aproximando do valor do limite que continua subindo ou descendo sem limites, então o limite não existe. Por favor, clique na imagem para uma melhor compreensão.

Se o gráfico estiver se aproximando de dois números diferentes de duas direções diferentes, à medida que x se aproxima de um determinado número, o limite não existe. Não podem ser dois números diferentes. Por favor, clique na imagem para uma melhor compreensão.