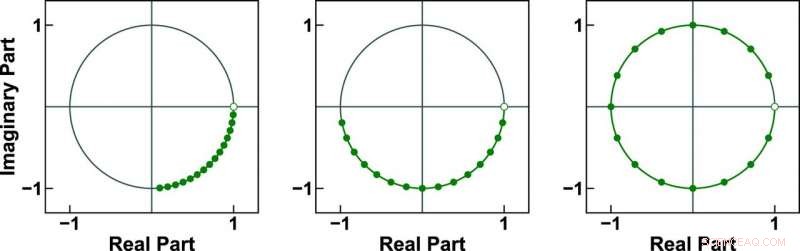
Aqui estão três exemplos de contornos de chirp de 16 pontos no círculo unitário. O algoritmo ICZT desenvolvido por engenheiros do estado de Iowa pode trabalhar com todos os três, enquanto o usado anteriormente pode funcionar apenas com o último contorno. Crédito:Alexander Stoytchev.
Alexander Stoytchev, da Iowa State University, diz que é um dos algoritmos "mais populares e úteis", embora a maioria de nós nunca tenha ouvido falar dele.
Mas, se você usou um telefone celular, navegou na internet ou precisava de uma imagem médica, você se beneficiou da transformação rápida de Fourier (FFT).
A transformação e seu inverso (conhecido como IFFT) estão em uso desde 1965. Por exemplo, no seu celular o FFT é usado para analisar o sinal recebido da estação base (ou torre de celular). O IFFT resolve o problema inverso:ele sintetiza o sinal que seu telefone envia para a estação base.
Em 1969, pesquisadores desenvolveram um método mais útil, versão generalizada da FFT conhecida como transformada z chirp (CZT). Mas ninguém apareceu com uma versão generalizada do IFFT. Era um quebra-cabeça de 50 anos no processamento de sinais.
Isso é, até o outono passado, quando dois engenheiros do estado de Iowa - Stoytchev e Vladimir Sukhoy - anunciaram em um artigo de pesquisa que haviam criado uma solução de forma fechada para a transformada z de chirp inversa (ICZT) e um algoritmo rápido para computá-la. (O artigo despertou muito interesse na comunidade de processamento de sinais, contabilizando mais de 26, 000 acessos desde outubro.)
Agora Stoytchev - professor associado de engenharia elétrica e da computação que também é afiliado ao Centro de Aplicações de Realidade Virtual da universidade - e Sukhoy - professor de engenharia elétrica e da computação - relatam novos resultados de pesquisa sobre seu algoritmo.
Em um artigo publicado online recentemente por Relatórios Científicos , um jornal Nature Research, os dois mostram como seu algoritmo funciona "no círculo unitário, "que se refere a um caso especial de seus parâmetros. (O artigo anterior apenas destacou as operações" fora do círculo unitário ".)
O artigo detalha como o algoritmo pode trabalhar com componentes de frequência que são gerados por pontos de amostra do círculo unitário no plano complexo. Esses pontos formam um contorno conhecido como contorno chirp. Ao contrário do IFFT, que só pode funcionar com pontos de amostragem equidistantes que cobrem totalmente o círculo unitário, o algoritmo ICZT pode trabalhar com contornos que cobrem apenas uma fração do círculo unitário. Ele também pode trabalhar com contornos que envolvem e realizam várias revoluções sobre o círculo. Isso permite o uso de certos componentes de frequência (não ortogonais), o que levanta uma das principais restrições do IFFT e pode levar a uma melhor utilização do espectro.
O artigo identifica os valores dos parâmetros para os quais o algoritmo é numericamente preciso e para os quais não é, e descreve como estimar sua precisão em função dos parâmetros. (Nota técnica:mostra que as singularidades do ICZT de tamanho n estão relacionadas aos elementos da sequência de Farey de ordem n-1. Esta é uma conexão interessante porque as sequências de Farey freqüentemente aparecem na teoria dos números.)
O artigo demonstra que, no círculo unitário, o algoritmo ICZT atinge alta precisão com apenas números de ponto flutuante de 64 bits e não requer precisão numérica adicional, tornando mais fácil de implementar. Ele relata que o algoritmo pode emparelhar bem com o algoritmo CZT existente para fazer análise de sinal back-to-back e síntese de sinal. E mostra que o algoritmo é rápido (ele opera no que é conhecido como tempo O (n log n)).
"Este algoritmo é mais geral do que o IFFT, mas mantém a mesma velocidade, "Stoytchev disse.
Essa é uma boa notícia para os engenheiros que trabalham para resolver todos os tipos de desafios de processamento de sinal:
"Domínios de aplicativos que poderiam se beneficiar com isso, "os engenheiros do estado de Iowa escreveram no jornal, "incluem processamento de sinal, eletrônicos, imagens médicas, radar, sonar, comunicações sem fio, e outros."