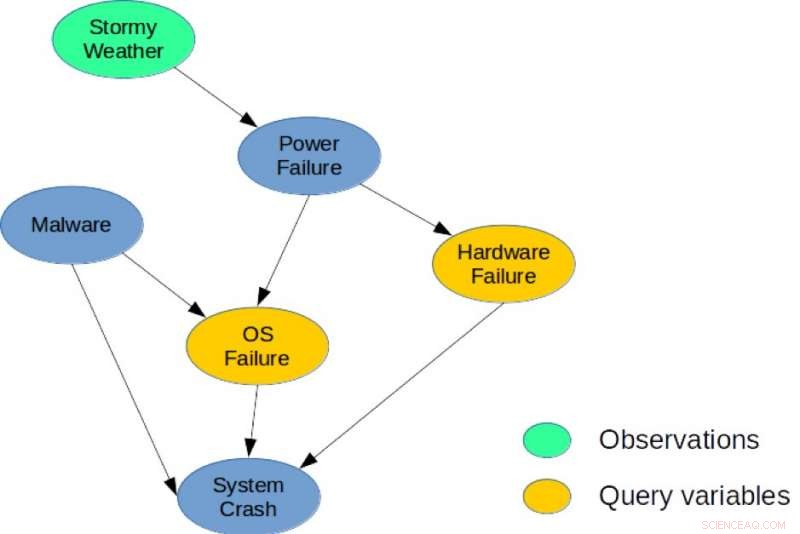
Figura 1. Uma rede bayesiana simples para uma tarefa de diagnóstico do sistema. Crédito:IBM
Existe uma profunda conexão entre planejamento e inferência, e na última década, vários pesquisadores introduziram reduções explícitas que mostram como o planejamento estocástico pode ser resolvido usando a inferência probabilística com aplicações em robótica, agendamento, e problemas ambientais. Contudo, métodos heurísticos e busca ainda são as abordagens de melhor desempenho para o planejamento em grandes espaços combinatórios de estado e ação. Meus co-autores e eu adotamos uma nova abordagem em nosso artigo, "Do planejamento estocástico ao mapa marginal" (autores:Hao Cui, Radu Marinescu, Roni Khardon), na Conferência sobre Sistemas de Processamento de Informação Neural (NeurIPS) de 2018, mostrando como as ideias do planejamento podem ser usadas para inferência.
Desenvolvemos o Solver baseado em gradiente algébrico (AGS), um novo solucionador para inferência de MAP marginal aproximada. O algoritmo constrói um gráfico de computação algébrica aproximado capturando marginais de variáveis de estado e recompensa sob suposições de independência. Em seguida, ele usa a diferenciação automática e a pesquisa baseada em gradiente para otimizar a escolha da ação. Nossa análise mostra que o valor calculado pelo gráfico de computação AGS é idêntico à solução de Propagação de Crenças (BP) quando condicionado a ações. Isso fornece uma conexão explícita entre algoritmos de planejamento heurístico e inferência aproximada.
Mais especificamente, revisitamos a conexão entre o planejamento estocástico e a inferência probabilística. Propomos pela primeira vez o uso de um algoritmo heurístico eficiente que foi projetado originalmente para resolver problemas de planejamento para lidar com uma tarefa de inferência central para modelos gráficos probabilísticos, ou seja, a tarefa de probabilidade marginal máxima a posteriori (MMAP).
Modelos gráficos probabilísticos, como redes Bayesianas ou redes de Markov, fornecem uma estrutura muito poderosa para raciocinar sobre estruturas de dependência condicional sobre muitas variáveis. Para esses modelos, a consulta de inferência MMAP é uma tarefa particularmente difícil, mas importante, correspondendo a encontrar a configuração mais provável (ou maximizar a probabilidade) em um subconjunto de variáveis, chamadas de variáveis MAP, depois de marginalizar (ou somar) o restante do modelo.
A inferência MMAP surge em muitas situações, especialmente em tarefas de diagnóstico e planejamento, em que a especificação mais natural do modelo contém muitas variáveis cujos valores não nos importamos em prever, mas que criam interdependência entre as variáveis de interesse. Por exemplo, em uma tarefa de diagnóstico baseada em modelo, dadas observações, buscamos otimizar um subconjunto de variáveis de diagnóstico que representam componentes potencialmente falhos em um sistema.
Para ilustração, considere a rede bayesiana mostrada na Figura 1, que descreve um problema de diagnóstico simples para um sistema de computação. O modelo captura dependências causais diretas entre seis variáveis aleatórias usadas para descrever este problema. Especificamente, uma falha de sistema pode ser causada por uma falha de hardware, uma falha de sistema operacional, ou a presença de malware no sistema. De forma similar, uma falha de energia pode ser causa comum de falha de hardware e sistema operacional, e o clima tempestuoso pode causar queda de energia. Uma possível consulta MMAP seria calcular a configuração mais provável de falhas de hardware e sistema operacional, visto que observamos o clima tempestuoso, independentemente do estado das outras variáveis (malware, Falha do sistema, ou falha de energia).
Estruturas de planejamento estocásticas, como processos de decisão de Markov, são amplamente utilizadas para modelar e resolver tarefas de planejamento em condições de incerteza. O planejamento de horizonte finito pode ser capturado usando uma rede Bayesiana dinâmica (DBN) onde as variáveis de estado e ação em cada etapa de tempo são representadas explicitamente e as distribuições de probabilidade condicional das variáveis são dadas pelas probabilidades de transição. No planejamento off-line, a tarefa é calcular uma política que otimize a recompensa a longo prazo. Em contraste, no planejamento on-line, temos um tempo fixo limitado t por etapa e não podemos calcular uma política com antecedência. Em vez de, dado o estado atual, o algoritmo deve decidir sobre a próxima ação dentro do tempo t. Em seguida, a ação é realizada, uma transição e recompensa são observadas e o algoritmo é apresentado com o próximo estado. Este processo se repete e o desempenho de longo prazo do algoritmo é avaliado.
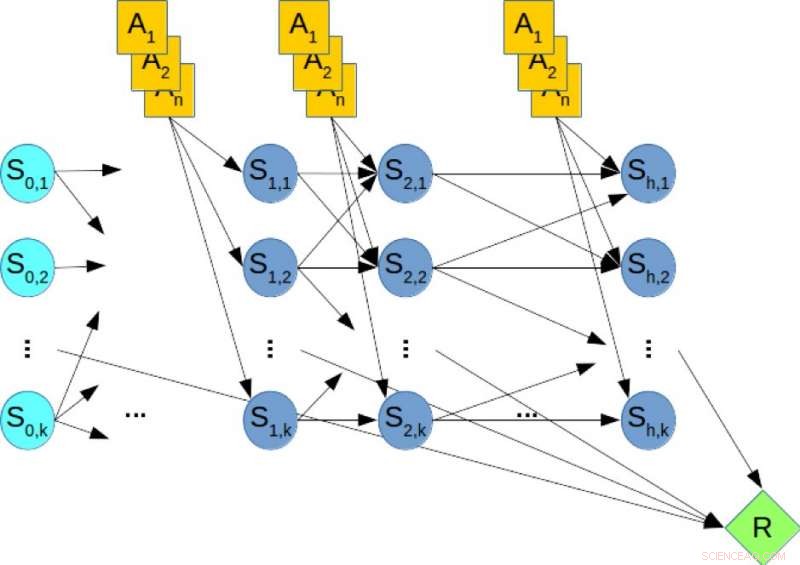
Figura 2. Uma rede Bayesiana dinâmica (DBN) para planejamento estocástico. Crédito:IBM
Para ilustração, considere a Figura 2, que mostra o DBN correspondente a um problema de planejamento hipotético, onde os nós laranja representam as variáveis de ação, os nós azuis denotam as variáveis de estado, e o nó verde denota a recompensa cumulativa que deve ser maximizada. Portanto, calcular a política ideal do problema de planejamento é equivalente a resolver uma consulta MMAP sobre o DBN, onde maximizamos as variáveis de ação e marginalizamos as variáveis de estado.
Nossa avaliação experimental de difíceis instâncias de problemas de MMAP mostra conclusivamente que o esquema AGS melhora o desempenho a qualquer momento de algoritmos de última geração em problemas de MMAP com subproblemas de soma total, às vezes em até uma ordem de magnitude. Acreditamos que essas conexões entre planejamento e inferência podem ser mais exploradas para produzir melhorias em ambos os campos.
Esta história foi republicada por cortesia da IBM Research. Leia a história original aqui.