
Figura 1:Expandindo os bairros a partir do nó marrom no meio. Primeira expansão:verde; segundo:amarelo; terceiro:vermelho.
Uma estrutura de gráfico é extremamente útil para prever propriedades de seus constituintes. A maneira mais bem-sucedida de realizar essa previsão é mapear cada entidade para um vetor por meio do uso de redes neurais profundas. Pode-se inferir a semelhança de duas entidades com base na proximidade do vetor. Um desafio para o aprendizado profundo, Contudo, é que é preciso reunir informações entre uma entidade e sua vizinhança expandida nas camadas da rede neural. A vizinhança se expande rapidamente, tornando a computação muito cara. Para resolver este desafio, propomos uma nova abordagem, validado por meio de provas matemáticas e resultados experimentais, que sugerem que é suficiente reunir as informações de apenas um punhado de entidades aleatórias em cada expansão de bairro. Esta redução substancial no tamanho da vizinhança processa a mesma qualidade de previsão que as redes neurais profundas de última geração, mas corta o custo de treinamento em ordens de magnitude (por exemplo, 10x a 100x menos tempo de computação e recursos), levando a uma escalabilidade atraente. Nosso artigo que descreve este trabalho, "FastGCN:Aprendizado rápido com redes convolucionais de grafos via amostragem de importância, "será apresentado no ICLR 2018. Meus co-autores são Tengfei Ma e Cao Xiao.
Complexidade da análise gráfica
Os gráficos são representações universais de relacionamento entre pares. Em aplicativos do mundo real, eles vêm em uma variedade de formas, incluindo, por exemplo, redes sociais, redes de expressão gênica, e gráficos de conhecimento. Um assunto em alta no aprendizado profundo é estender o notável sucesso de arquiteturas de rede neural bem estabelecidas para dados estruturados euclidianos (como imagens e textos) para dados estruturados irregularmente, incluindo gráficos. A rede convolucional do gráfico, GCN, é um exemplo excelente. Ele generaliza o conceito de convolução para imagens, que pode ser considerada uma grade de pixels, para gráficos que não se parecem mais com uma grade regular.
A ideia por trás do GCN é muito simples. Aqueles de nós que fizeram Signal Processing 101 ou um curso básico de visão computacional já estão familiarizados com o conceito de filtro de convolução. Para imagens, é uma pequena matriz de números, a ser multiplicado elemento a elemento com uma janela móvel da imagem, com a soma do produto resultante substituindo o número do centro da janela. Para gráficos, isso é semelhante. Uma boa combinação dos filtros pode detectar estruturas locais primitivas, como linhas em ângulos diferentes, arestas, cantos, e manchas de uma determinada cor. Para gráficos, as convoluções são semelhantes. Imagine que cada nó do grafo é inicialmente anexado a um vetor. Para cada nó, os vetores dos vizinhos são somados (com certos pesos e transformações) nele. Portanto, todos os nós são atualizados simultaneamente, realizando uma camada de propagação direta. As convoluções do grafo podem ser usadas para propagar informações através das vizinhanças, de modo que a informação global seja disseminada para cada nó do grafo.
O problema do GCN é que, para uma rede com várias camadas, a vizinhança é rapidamente expandida, envolvendo muitos vetores a serem somados, para apenas um único nó. Tal cálculo é proibitivamente caro para gráficos com um grande número de nós. Qual será o tamanho de uma vizinhança expandida? Na análise de redes sociais, existe um conceito famoso cunhado "seis graus de separação, "que afirma que se pode chegar a qualquer outra pessoa na Terra por meio de seis conexões intermediárias! A Figura 1 ilustra que, partindo do nó marrom no centro, expandindo a vizinhança três vezes (na ordem do verde, amarelo, e vermelho) tocará quase todo o gráfico. Em outras palavras, atualizar o vetor do nó marrom sozinho é problemático para um GCN com apenas três camadas.
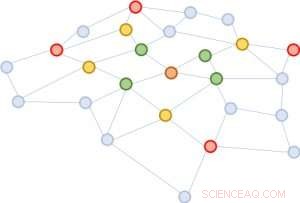
Figura 2:começando do mesmo nó marrom, em cada expansão de bairro, nós amostramos quatro nós apenas.
Simplificando para escalabilidade
Propomos uma solução simples, mas poderosa, chamado FastGCN. Se expandir totalmente a vizinhança custar caro, por que não expandir apenas alguns vizinhos de cada vez? A Figura 2 ilustra o conceito. A partir do nó marrom, em cada expansão, escolhemos um número constante (quatro) de nós e somamos os vetores apenas a partir deles. A amostragem reduz substancialmente o custo de treinamento da rede neural, reduzindo o tempo de treinamento em ordens de magnitude em conjuntos de dados de referência comumente usados por pesquisadores. Ainda, as previsões permanecem comparativamente precisas. O tamanho desses gráficos de referência varia de alguns milhares de nós a algumas centenas de milhares de nós, confirmando a escalabilidade do nosso método.
Por trás dessa abordagem intuitiva está uma teoria matemática para a aproximação da função de perda. Uma camada da rede pode ser resumida como uma multiplicação de matriz:H '=s (AHW), onde A é a matriz de adjacência do grafo, cada linha de H é o vetor anexado aos nós, W é uma transformação linear dos vetores (também interpretada como o parâmetro do modelo a ser aprendido), e as linhas de H 'contêm os vetores atualizados. Generalizamos esta multiplicação de matriz para uma transformação integral h '(v) =s (òA (v, u) h (u) W dP (u)) sob uma medida de probabilidade P. Então, a amostragem de um número fixo de vizinhos em cada expansão nada mais é do que uma aproximação de Monte Carlo da integral sob a medida P. A aproximação de Monte Carlo produz um estimador consistente da função de perda; portanto, tomando o gradiente, podemos usar um método de otimização padrão (como a descida gradiente estocástica) para treinar a rede neural.
Uma variedade de aplicativos de aprendizado profundo
Nossa abordagem aborda um desafio importante no aprendizado profundo para gráficos de grande escala. Ele se aplica não apenas ao GCN, mas também a muitas outras redes neurais de grafos construídas no conceito de expansão de vizinhança, um componente essencial do aprendizado de representação de grafos. Prevemos que a resolução do desafio nesta estrutura de dados fundamental - gráficos - será adotada em uma ampla gama de aplicações, incluindo a análise de redes sociais, o profundo conhecimento das interações proteína-proteína para a descoberta de medicamentos, e a curadoria e descoberta de informações em bases de conhecimento.