Origami computacional:um método universal para envolver superfícies curvas 3-D com materiais não extensíveis
 p Origami computacional de engenharia reversa para embalagem conforme. (A) Rugas são formadas ao envolver firmemente uma folha de papel retangular em torno de uma superfície gaussiana diferente de zero. (B) Os padrões de corte fractal podem evitar rugas, mas inevitavelmente levam a aberturas e áreas descobertas. (C) O desdobramento 2D de um poliedro esférico gerado automaticamente por origami computacional pode envolver uma bola de aço sem deixar áreas descobertas. (D) À medida que o número de facetas aumenta, a suavidade e a conformabilidade da malha melhoram naturalmente. A diferença na área de superfície entre a esfera perfeita e o poliedro aproximado diminui 5,3% quando o número de facetas aumenta de 80 para 500. A distância de Hausdorff entre as superfícies poliédricas e a esfera perfeita também reduz de 7,05 para 1,17% do raio de a esfera perfeita quando o número de facetas aumenta de 80 para 500 (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Origami computacional de engenharia reversa para embalagem conforme. (A) Rugas são formadas ao envolver firmemente uma folha de papel retangular em torno de uma superfície gaussiana diferente de zero. (B) Os padrões de corte fractal podem evitar rugas, mas inevitavelmente levam a aberturas e áreas descobertas. (C) O desdobramento 2D de um poliedro esférico gerado automaticamente por origami computacional pode envolver uma bola de aço sem deixar áreas descobertas. (D) À medida que o número de facetas aumenta, a suavidade e a conformabilidade da malha melhoram naturalmente. A diferença na área de superfície entre a esfera perfeita e o poliedro aproximado diminui 5,3% quando o número de facetas aumenta de 80 para 500. A distância de Hausdorff entre as superfícies poliédricas e a esfera perfeita também reduz de 7,05 para 1,17% do raio de a esfera perfeita quando o número de facetas aumenta de 80 para 500 (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p A pergunta contra-intuitiva sobre como envolver uma superfície esférica curva usando materiais convencionalmente rígidos e não esticáveis ou quebradiços, constitui a base deste estudo. Para responder a pergunta, Yu-Ki Lee e uma equipe de pesquisa nos departamentos de engenharia de materiais e ciência da computação na República da Coréia e nos EUA estenderam um método de design geométrico de origami computacional para envolver construções esféricas em um novo relatório agora publicado em
Avanços da Ciência . A abordagem forneceu um método robusto e confiável para projetar dispositivos conformes para superfícies curvas arbitrárias usando uma rede desenvolvível não poliédrica projetada computacionalmente. O projeto auxiliado por computador transformou materiais bidimensionais (2-D), como wafers de silício (Si) e chapas de aço em estruturas conformadas que poderiam envolver totalmente estruturas 3-D sem fratura ou deformação. O método de empacotamento computacional permitiu que eles desenvolvessem uma plataforma de projeto para transformar dispositivos 2-D convencionalmente não esticáveis em superfícies curvas 3-D conformadas. p O estudo introduziu um método universal para materiais não extensíveis convencionais para envolver superfícies curvas 3-D arbitrárias e diversas por dispositivos de material conformado de engenharia sem sacrificar seu desempenho. Por exemplo, embrulhar uma esfera com um pedaço de papel retangular pode inevitavelmente formar rugas, ao tentar embrulhar uma esfera com um substrato mais resistente pode causar a fratura do material de embrulho. Para facilitar o processo, cientistas de materiais podem introduzir cortes padronizados em materiais não extensíveis, incluindo padrões de corte de rede e padrões de corte fractal para envolver efetivamente superfícies 3-D. Esses conceitos são programáveis por forma e podem cobrir uma esfera com eficiência. Os engenheiros também recomendaram algoritmos de computador para projetar modelos 3-D complexos baseados em estruturas auxéticas 2-D. Para obter uma cobertura ideal, eles introduziram uma estratégia de design computacional conhecida como "empacotamento computacional com redes desenvolvíveis não poliédricas, "para formar plataformas de material não extensível para vestíveis e dispositivos conformados.
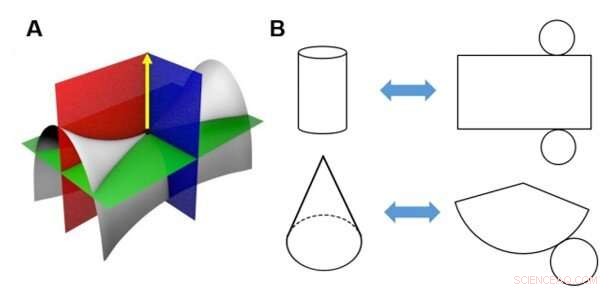 p Limitação matemática de envolver uma folha plana em torno de uma superfície 3D com curvaturas gaussianas diferentes de zero. (A) A curvatura gaussiana é o produto vetorial das curvaturas principais máxima e mínima em um ponto. No ponto de sela (ponto preto) da superfície cinza, uma das principais curvaturas é a interseção entre as superfícies vermelha e cinza, e a outra é a interseção entre as superfícies azul e cinza. Os planos vermelho e azul contêm o vetor normal do ponto de sela, e suas intersecções com a superfície cinza definem as curvaturas principais. Um material 2D com zero pontos de curvatura gaussiana, como uma folha de papel, é chamada de "superfície desenvolvível", que não pode ser transformada em uma superfície 3D com uma curvatura gaussiana positiva ou negativa (ou seja, uma “superfície não revelável”) sem esticar ou comprimir. (B) Por exemplo, um cilindro ou cone pode ser coberto com papel cortado, mas uma sela ou uma esfera não podem ser enroladas sem a formação de rugas ou cortes. O processo reverso (achatamento) também é o mesmo, é por isso que existem distorções no mapa planar da Terra. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Limitação matemática de envolver uma folha plana em torno de uma superfície 3D com curvaturas gaussianas diferentes de zero. (A) A curvatura gaussiana é o produto vetorial das curvaturas principais máxima e mínima em um ponto. No ponto de sela (ponto preto) da superfície cinza, uma das principais curvaturas é a interseção entre as superfícies vermelha e cinza, e a outra é a interseção entre as superfícies azul e cinza. Os planos vermelho e azul contêm o vetor normal do ponto de sela, e suas intersecções com a superfície cinza definem as curvaturas principais. Um material 2D com zero pontos de curvatura gaussiana, como uma folha de papel, é chamada de "superfície desenvolvível", que não pode ser transformada em uma superfície 3D com uma curvatura gaussiana positiva ou negativa (ou seja, uma “superfície não revelável”) sem esticar ou comprimir. (B) Por exemplo, um cilindro ou cone pode ser coberto com papel cortado, mas uma sela ou uma esfera não podem ser enroladas sem a formação de rugas ou cortes. O processo reverso (achatamento) também é o mesmo, é por isso que existem distorções no mapa planar da Terra. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Em teoria, os pesquisadores podem caracterizar uma superfície curva pela curvatura gaussiana - que é o produto vetorial das curvaturas principais máxima e mínima em um ponto. Por exemplo, uma folha de papel é chamada de 'superfície revelável' e representa um material 2-D com curvatura gaussiana zero em todos os pontos. Uma superfície revelável não pode ser transformada em uma superfície 3-D não revelável sem rasgar, esticar ou comprimir o material. O conceito é matematicamente comprovado pelo "Gauss Theorema Egregium, "que afirma que" Para mover uma superfície para outra superfície, a curvatura gaussiana de todos os pontos correspondentes deve coincidir. "Os cientistas da computação têm feito grandes esforços para determinar algoritmicamente os cortes de superfície que segmentam uma superfície não desenvolvível em manchas de superfície desenvolvíveis conhecidas como redes poliédricas ou simplesmente - Métodos computacionais recentes têm como objetivo otimizar a qualidade e dobrabilidade da rede usando métodos de aprendizado de máquina, a fim de reduzir o tempo e o esforço necessários para as abordagens tradicionais de tentativa e erro.
p Como a maioria dos objetos 3D do mundo real são suaves e curvos, os cientistas exigem malhas de alta resolução para cobrir as superfícies com precisão. Nesse trabalho, Lee et al. desenvolveu uma nova abordagem conhecida como "empacotamento computacional" que vai além do método convencional de dobramento computacional. Para conseguir isso, eles consideraram o design de dispositivo conforme como um problema de embrulho de papel em vez de um desafio de dobradura de papel (origami). A equipe reconheceu as funções de anexar e envolver dispositivos conformados para cobrir uma superfície 3-D curva subjacente, simplesmente dobrando e pressionando uma rede poliédrica sem vincos.
 p Conceito e demonstração física de empacotamento computacional. (A) Quando a soma dos ângulos de dobramento de uma rede é minimizada, as linhas de vinco podem ser ignoradas para acomodar materiais rígidos e quebradiços flexíveis, mas não extensíveis. Para 500 malhas, as lacunas no caso de um material rígido e as rugas no caso de um material flexível não são mais visíveis, e a diferença entre os dois torna-se imperceptível. (B) Uma folha de aço inoxidável não extensível é cortada em uma rede revelável. (C) Com um número suficiente de malhas, a folha de aço inoxidável pode ser dobrada e envolver totalmente uma esfera sem vincar ou dobrar. (D) Parte da esfera é desdobrada com 400 malhas, e as linhas de vinco são removidas. (E) Um wafer quebradiço de Si com 20 μm de espessura é cortado em uma rede desdobrada com um cortador a laser. (F) O wafer de Si cortado envolve de forma estável os quadros convexo e côncavo. (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Conceito e demonstração física de empacotamento computacional. (A) Quando a soma dos ângulos de dobramento de uma rede é minimizada, as linhas de vinco podem ser ignoradas para acomodar materiais rígidos e quebradiços flexíveis, mas não extensíveis. Para 500 malhas, as lacunas no caso de um material rígido e as rugas no caso de um material flexível não são mais visíveis, e a diferença entre os dois torna-se imperceptível. (B) Uma folha de aço inoxidável não extensível é cortada em uma rede revelável. (C) Com um número suficiente de malhas, a folha de aço inoxidável pode ser dobrada e envolver totalmente uma esfera sem vincar ou dobrar. (D) Parte da esfera é desdobrada com 400 malhas, e as linhas de vinco são removidas. (E) Um wafer quebradiço de Si com 20 μm de espessura é cortado em uma rede desdobrada com um cortador a laser. (F) O wafer de Si cortado envolve de forma estável os quadros convexo e côncavo. (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Malhas de alta resolução permitiram que eles atendessem aos limites de longos tempos de fabricação e confiabilidade mecânica. Para encerrar uma superfície com curvatura gaussiana não nula geral, como uma esfera perfeita, Lee et al. usou uma superfície revelável após refinar a malha da faceta para atender aos valores exigidos de estanqueidade do envoltório. Os resultados forneceram dados sobre uma rede desenvolvível não poliédrica para criar espaços controlados e limitados entre a rede e a esfera sem lacunas ou sobreposições entre as facetas. O processo de fabricação produziu com precisão superfícies 3-D suaves e altamente complexas, muitas vezes mais rápido do que os métodos convencionais de dobra computacional ao lidar com formas complexas usando papel, materiais de embalagem metálicos e cerâmicos. A análise de elementos finitos confirmou que tais invólucros computacionais eram mecanicamente confiáveis.
 p Simulação de elemento finito (FE) para envolver uma esfera com um wafer de Si de 100 µm de espessura com uma rede desenvolvível não poliédrica. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Simulação de elemento finito (FE) para envolver uma esfera com um wafer de Si de 100 µm de espessura com uma rede desenvolvível não poliédrica. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p As estruturas desenvolvidas no trabalho levaram a um aumento significativo no origami computacional para processos de fabricação industrial do mundo real. Por exemplo, Lee et al. desenvolveu um dispositivo conformal usando painéis de lâmpada eletroluminescente (EL) para envolver uma esfera, o dispositivo conformado 3-D resultante exibiu boa função e eles creditaram os resultados aos processos de dobra e prensagem usados para embrulhar a esfera, em vez das técnicas de vincar e dobrar. A equipe também demonstrou seu método em uma máscara comercial coreana e em um veículo elétrico de brinquedo com painéis EL conectados para funcionar sem falhas. Para gerar a rede desenvolvível para componentes com superfícies gaussianas diferentes de zero, como os faróis do veículo elétrico de brinquedo, os cientistas usaram o método de desdobramento do algoritmo genético (GA).
 p Demonstração de dispositivos conformes. (A) Cortável, não extensível, Painéis EL comerciais consistindo de eletrodos quebradiços são cortados com um cortador a laser para formar redes reveláveis para uma esfera. (B) Os painéis EL com uma rede desenvolvível podem cobrir totalmente uma esfera e (C) operar sem falha catastrófica. (D e E) O conceito de empacotamento computacional também é demonstrado para um modelo elipsóide. (F e G) Além de uma esfera e um elipsóide, uma máscara facial coreana comercial também pode ser conformavelmente coberta com painéis EL e operada sem falha elétrica. (H) Um veículo de brinquedo elétrico também pode ser embalado de forma conformada com painéis EL da mesma maneira, e os painéis EL anexados também funcionam bem sem falhas. O método de desdobramento GA é usado para gerar a rede desenvolvível para peças com superfícies gaussianas diferentes de zero, incluindo (I) os faróis, a borda do pára-choque frontal, e (J) a borda do pára-choque lateral traseiro do veículo elétrico de brinquedo. (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul.) Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Demonstração de dispositivos conformes. (A) Cortável, não extensível, Painéis EL comerciais consistindo de eletrodos quebradiços são cortados com um cortador a laser para formar redes reveláveis para uma esfera. (B) Os painéis EL com uma rede desenvolvível podem cobrir totalmente uma esfera e (C) operar sem falha catastrófica. (D e E) O conceito de empacotamento computacional também é demonstrado para um modelo elipsóide. (F e G) Além de uma esfera e um elipsóide, uma máscara facial coreana comercial também pode ser conformavelmente coberta com painéis EL e operada sem falha elétrica. (H) Um veículo de brinquedo elétrico também pode ser embalado de forma conformada com painéis EL da mesma maneira, e os painéis EL anexados também funcionam bem sem falhas. O método de desdobramento GA é usado para gerar a rede desenvolvível para peças com superfícies gaussianas diferentes de zero, incluindo (I) os faróis, a borda do pára-choque frontal, e (J) a borda do pára-choque lateral traseiro do veículo elétrico de brinquedo. (Crédito da foto:Y.-K. Lee, Universidade Nacional de Seul.) Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
p Desta maneira, Yu-Ki Lee e seus colegas introduziram o conceito de empacotamento computacional para converter dispositivos flexíveis 2-D não extensíveis em dispositivos conformados 3-D. Usando o método, eles encerraram uma superfície com curvatura gaussiana diferente de zero, como uma esfera perfeita. A técnica proposta poderia controlar a distância entre as duas superfícies para garantir um envolvimento firme. O trabalho produziu uma única superfície conectada conhecida como rede desenvolvível não poliédrica, projetado para embrulhar conformally uma folha 2-D para qualquer superfície 3-D. Como resultado, os cientistas conseguiram até mesmo facilitar que materiais rígidos e frágeis, como folhas de metal e wafers de Si, cobrissem totalmente e envolvessem superfícies com curvatura gaussiana diferente de zero. O método de empacotamento computacional universal desenvolvido neste trabalho fornecerá novos insights sobre o desenvolvimento de dispositivos conformes com formas arbitrárias usando algoritmos eficientes e robustos, métodos de fabricação confiáveis. p © 2020 Science X Network




