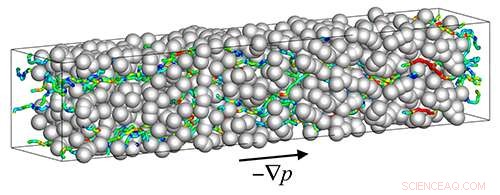
Fig.1:Linhas aerodinâmicas de fluxo de gás através de um meio poroso induzido pelo gradiente de pressão aplicado ∇p. A cor das linhas de corrente representa a força da velocidade do fluxo, onde o vermelho representa a velocidade rápida e o azul representa a velocidade lenta. Crédito:Tohoku University
Os cientistas desenvolveram expressões matemáticas que estimam com mais precisão o movimento do gás através de poros nanométricos. Isso pode ajudar a melhorar o desenvolvimento de células de combustível.
Muitos dispositivos projetados dependem do fluxo de gases através de um meio poroso. Em conversores catalíticos, por exemplo, gases nocivos de exaustão de automóveis passam por um meio poroso de grânulos de cerâmica revestidos com um catalisador que os converte em compostos inofensivos. Também, em células de combustível em desenvolvimento para veículos ecológicos, hidrogênio e oxigênio passam por um catalisador poroso que os converte em água, produção de eletricidade.
Os engenheiros precisam de uma compreensão clara de como os gases se movem através de meios porosos para melhorar esses dispositivos. Contudo, é difícil medir o transporte de moléculas através de poros nanométricos.
Pesquisadores da Universidade Tohoku no Japão, especializados em dinâmica de gases rarefeitos, junto com colegas da Honda R&D Co., Ltd., usou simulações baseadas em computador para desenvolver duas expressões matemáticas que estimam a velocidade do fluxo de gás através de um meio poroso.
As expressões parecem equações, mas realmente mostram uma relação física entre a velocidade do fluxo através de um meio poroso e gradiente de pressão, que pode ajudar na compreensão do transporte molecular através de meios porosos. Isso poderia ajudar no desenvolvimento de células de combustível mais ecologicamente corretas para carros e até mesmo para futuros ônibus espaciais.
A equipe usou o método 'simulação direta Monte Carlo (DSMC), 'que modela o fluxo de gás de baixa pressão usando moléculas de simulação. Em seu estudo, os meios porosos foram representados por partículas esféricas sólidas dispostas aleatoriamente. A equipe investigou o que aconteceu quando um fluxo constante de moléculas de hidrogênio foi conduzido através do meio por um gradiente de pressão constante. Simulações foram realizadas para diferentes porosidades e diferentes tamanhos de partículas sólidas.
A equipe descobriu que a velocidade do fluxo de gás através de um meio poroso aumenta em proporção ao gradiente de pressão crescente. Isso mostra que a lei de Darcy, que afirma que a taxa de fluxo de fluido através de um meio poroso é proporcional ao gradiente de pressão, aplica-se mesmo com poros nanométricos. Contudo, eles encontraram modelos convencionais, como a equação Kozeny-Carman, que é frequentemente usado para estimar a velocidade do fluxo através de um meio poroso, produziu estimativas que eram diferentes dos resultados das simulações DSMC quando os poros microsized foram trocados por poros nanosized.
Quando os poros são relativamente grandes, a diferença de pressão induz o fluxo de gás. O fluxo estabiliza quando a força viscosa exercida sobre o gás nas paredes dos poros equilibra a força devido à diferença de pressão. Isso é chamado de 'fluxo viscoso'. Por outro lado, quando os poros são nanodimensionados, as moléculas de gás não podem sentir a diferença de pressão diretamente porque as colisões molécula a molécula são muito menos frequentes em comparação com as colisões molécula a parede. Nesse caso, as moléculas de gás se espalham em direções aleatórias após as colisões entre as moléculas. Esses movimentos moleculares caóticos induzem um fluxo molecular líquido na direção de menor concentração. Isso é chamado de 'fluxo de Knudsen'. A razão pela qual os modelos convencionais produziram estimativas imprecisas no caso de poros nanométricos é porque apenas o fluxo viscoso é considerado nesses modelos.
A equipe desenvolveu duas expressões matemáticas que descrevem a velocidade do fluxo de gás através de um meio poroso. Eles consideravam um meio poroso como um feixe de tubos capilares tortuosos, cujo diâmetro é igual à distância média que uma molécula viaja entre sucessivas colisões molécula-parede. Suas expressões para um meio poroso foram construídas sobrepondo as contribuições de fluxos viscosos e de Knudsen através dos tubos capilares tortuosos.
A equipe descobriu que inserir informações como diâmetro de partícula e porosidade nessas expressões resultou em estimativas de velocidade de fluxo que concordaram bem com os resultados da simulação do DSMC.
"Nossas expressões serão aplicáveis a qualquer gás com moléculas simples e a qualquer meio poroso com uma estrutura interna arbitrária, "diz Shigeru Yonemura da Universidade de Tohoku, o autor correspondente do estudo. “Esse conhecimento será útil não só para as tecnologias de células de combustível, mas também para qualquer tecnologia que envolva fluxo de gás por meio poroso. Nosso próximo passo é construir uma expressão teórica para a tortuosidade do tubo capilar. Com isso, poderemos completar nossas expressões para estimar as velocidades de fluxo de gás através de qualquer meio poroso. "