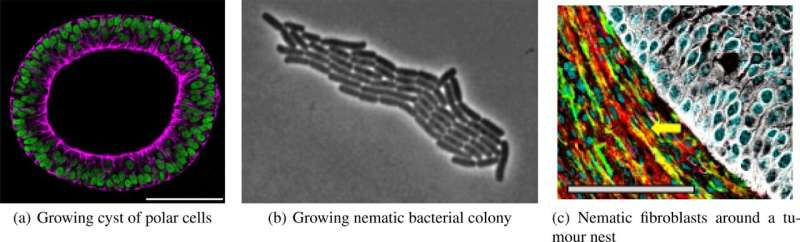
um cisto crescente de células polares. A polaridade induz uma anisotropia no crescimento, que por sua vez cria tensões que têm um efeito de feedback sobre o crescimento. b Colônia bacteriana em crescimento. A natureza nemática das bactérias leva a uma estrutura específica na colônia e no campo polar. c As células cancerígenas podem não ter uma ordem polar ou nemática intrínseca. No entanto, nos tumores desmoplásicos, o ambiente é altamente ordenado, como mostrado aqui com os fibroblastos que circundam um ninho de tumor pulmonar. Crédito:The European Physical Journal Plus (2023). DOI:10.1140/epjp/s13360-023-04669-9 Uma característica fundamental dos tecidos biológicos é a sua falta de homogeneidade e a sua capacidade de crescer através da reprodução celular. Para estudar esse comportamento, é importante descrevê-lo por meio de equações, que levam em conta fatores que incluem taxas de crescimento, sinalização química e estrutura do tecido.
Pesquisadores de Paris pretendem desenvolver descrições contínuas e consistentes desses sistemas profundamente complexos:prevendo com precisão propriedades como taxas de reprodução celular, desordem e como seu crescimento varia em diferentes direções do espaço, dependendo de suas interações.
Através da sua nova análise publicada no The European Physical Journal Plus , Joseph Ackermann e Martine Ben Amar, da Sorbonne University Paris, mostram que o desenvolvimento do tecido pode ser capturado de forma confiável dentro do "princípio variacional de Onsager", uma estrutura matemática amplamente utilizada na termodinâmica.
A sua abordagem poderia levar a uma compreensão mais profunda das propriedades dos tecidos numa vasta gama de cenários, desde processos essenciais, como o desenvolvimento embrionário, até processos prejudiciais, como o crescimento de tumores.
Na termodinâmica, o princípio variacional de Onsager descreve como os sistemas tendem a um estado de dissipação mínima à medida que são continuamente alterados por suas próprias transformações e pelo ambiente. Matematicamente, o princípio expressa estes sistemas como grupos de equações interligadas, cada uma descrevendo as taxas de variação de certas quantidades que as descrevem.
A partir do princípio variacional de Onsager, são derivadas novas equações de "momento" e de crescimento, que poderiam descrever melhor o fluxo de massa e a proliferação, bem como as orientações das células nos tecidos biológicos. Suas equações consideraram as taxas de crescimento e morte das células, bem como as reações químicas que impulsionam sua atividade. Esta abordagem também poderia ilustrar a gênese de padrões em órgãos em crescimento.
Ao todo, o trabalho da dupla mostra definitivamente como o princípio variacional de Onsager pode ser uma ferramenta valiosa para explorar diferentes cenários teóricos em tecidos em crescimento, e como o seu crescimento depende de interações entre diferentes propriedades em escala celular.
