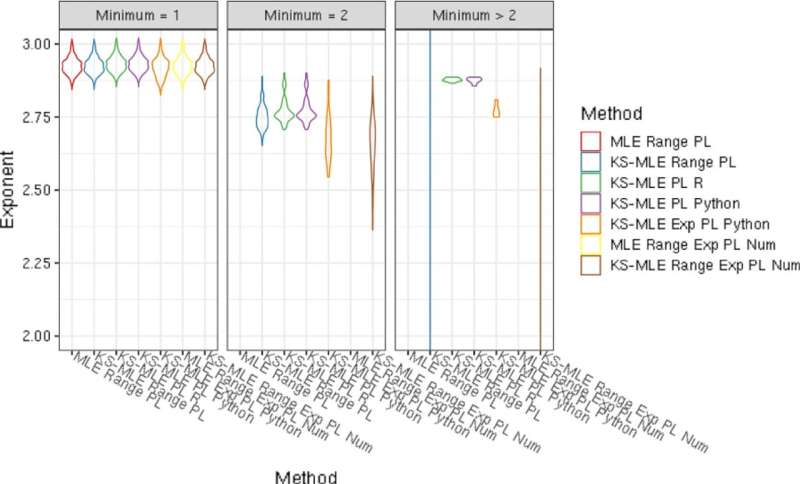
Distribuição de expoentes de lei de potência para vários métodos de ajuste. As leis de potência são ajustadas a um processo de coalescência e fragmentação simulado com núcleos com tendência de tamanho como em (2, 3), M =10
4
, F =0,3 e 20.000 amostras. Escrevemos MLE e KS-MLE como no texto principal, “PL” para lei de potência, “Range” para intervalo finito, “Exp” para um corte exponencial, “R” para o pacote poweRlaw, “Python” para o pacote powerlaw e “Num” para a estimativa numérica de máxima verossimilhança no pacote bbmle. O valor teórico é 2,5, do qual todos os métodos se desviaram com níveis variados de viés. Crédito:The European Physical Journal B (2024). DOI:10.1140/epjb/s10051-024-00654-y Em 1960, Lewis Fry Richardson observou a famosa observação de que a gravidade de um evento em tempo de guerra é descrita por uma distribuição simples da lei de potência que aumenta de acordo com o tamanho do conflito. Desde então, os estatísticos propuseram várias modificações, mas continuam a concordar que o número de vítimas num conflito violento tende a aumentar com o tamanho do grupo insurgente que causou o conflito.
Em um estudo publicado no The European Physical Journal B , Brennen Fagan, da Universidade de York, Reino Unido, e seus colegas analisam modelos de como sistemas complexos se aglutinam e se fragmentam com base nessas dinâmicas de guerra. Seu trabalho avalia a robustez desses modelos e elucida a relação entre a dinâmica microscópica e os fenômenos observados.
Em populações finitas, os grupos se aglutinam e se fragmentam. Esses processos tendem a se equilibrar, resultando em grupos cuja distribuição de tamanho é descrita por uma lei de potência. Fagan supôs que estas distribuições observadas resultam da mesma auto-organização básica que molda os conflitos humanos.
Os sistemas complexos também apresentam mudanças em escala mais refinada nas distribuições dos grupos:gelificação, onde a maior parte da população é absorvida por um único grande grupo, e fragmentação, onde grandes grupos se dividem em indivíduos. Além disso, os modelos sugerem um fenómeno emergente:ciclos estocásticos de gelificação e fragmentação.
Fagan e seus colegas realizaram simulações para examinar como os modelos padrão de coalescência e fragmentação variam com diferentes regras subjacentes ou adicionais comuns às aplicações. Eles descobriram que a distribuição básica da lei de potência persistia quando os indivíduos mudavam de e para grupos escolhidos aleatoriamente e com destruição parcial em vez de total. Mas para distribuições mais amplas de tamanhos de fragmentos, a ciclicidade de quebra de gel não ocorreu mais.
Os resultados deverão ser aplicáveis a uma ampla variedade de sistemas, desde as interacções físicas entre asteróides e poeira até estruturas probabilísticas, económicas, biológicas e sociais – como a guerra insurgente que inspirou a análise.
A pesquisa foi publicada no The European Physical Journal B .
