Um par de pesquisadores da Universit'e Paris-Saclay, CNRS e Univ Rennes, CNRS, IPR, respectivamente, usou a matemática para ajudar a descrever o processo envolvido quando fios curtos de fibra são torcidos em longos trechos de fio. Em seu artigo publicado na revista Physical Review Letters, Antoine Seguin e Jérôme Crassous descrevem como usaram experimentos e simulações para entender melhor os fatores envolvidos quando as fibras são torcidas juntas.
Os humanos torcem pequenos fios de fibras para criar longos fios de corda ou fio há milhares de anos e, embora o processo geral seja bem compreendido, a matemática por trás dele tem sido bastante incompleta. Nesse novo esforço, Seguin e Crassous abordaram o problema usando uma nova abordagem, aplicando experimentos e simulações.

À medida que várias fibras curtas são torcidas juntas, elas se entrelaçam, mas é claro que isso não é suficiente para mantê-las juntas. Eles se mantêm juntos por causa do atrito envolvido. Puxar as extremidades de um pedaço de fio força os fios individuais de que é feito a empurrar uns contra os outros, aumentando a quantidade de atrito e, portanto, sua força. Mas existem regras matemáticas que regem o processo? Qual é o número ideal de fibras, por exemplo, para garantir o fio mais forte? Ou que grau de resistência é dado ao fio pelo grau de atrito entre dois fios de fibra?

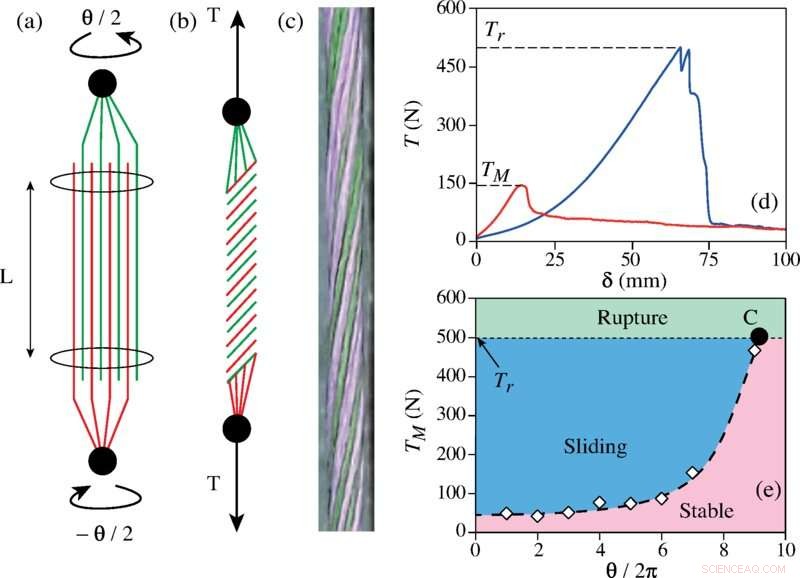
Para encontrar essas respostas, os pesquisadores realizaram vários testes em diferentes fibras torcidas em fios. Eles descobriram que um aumento nas torções aumentava a força de ligação da fibra – mas apenas até certo ponto. Além disso, cada tipo de fibra tinha seu próprio ponto de ruptura. Ao criar simulações para testar mais facilmente diferentes configurações, eles também descobriram que havia um raio de fibra ideal para um determinado comprimento de fio e que a resistência do fio era dimensionada com o exponencial do quadrado do ângulo de torção.

Ao procurar semelhanças, eles descobriram o que descrevem como o número de torção de Hercules – um parâmetro que descreve as forças envolvidas com o ângulo de torção, um coeficiente de atrito e o raio do fio. Eles também descobriram que esse número em geral era proporcional ao quadrado do número de torções aplicadas e tinha um valor crítico de 30. Eles também desenvolveram uma fórmula para mostrar o tamanho ideal do raio para um determinado tipo de fibra. + Explorar mais

Pesquisadores investigam 'por que as roupas não desmoronam'

© 2022 Science X Network