Novo modelo descreve puffs, slugs e o papel da aleatoriedade na turbulência transicional
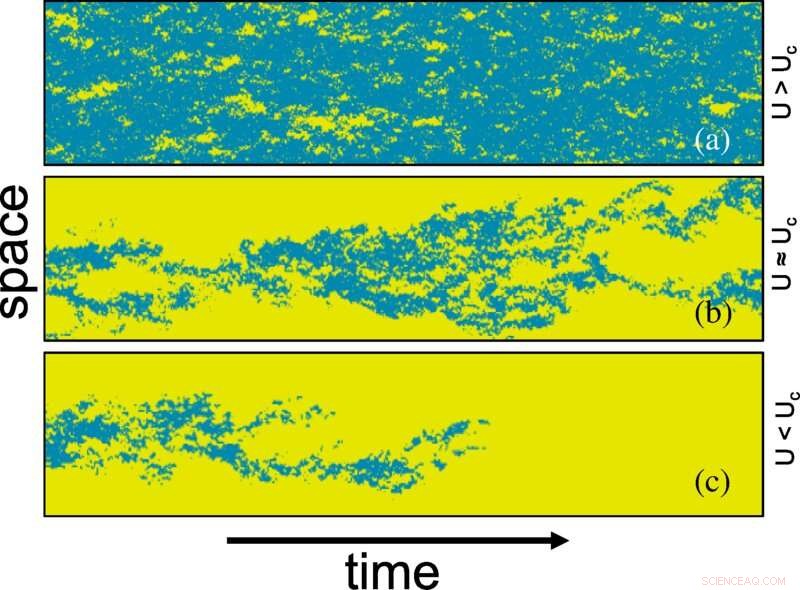
Gráfico espaço-tempo da transição laminar-turbulenta em função de U (ou seja, número de Reynolds) gerado pelo modelo PP em fluxo quase-1D Taylor-Couette. A turbulência (em azul) é representada pela densidade de presas B, gerada por simulação de Monte Carlo em uma rede 2D de tamanho 20×3000 (a) abaixo do ponto crítico U=0,0135 , (b) no ponto crítico U=0,01425 , e (c) acima do ponto crítico U=0,0165 . Amarelo representa a fase laminar localmente desocupada pela presa. A densidade da presa é binarizada de acordo com o fato de ser maior que 0,065× a densidade máxima da presa. Crédito:Cartas de Revisão Física (2022). DOI:10.1103/PhysRevLett.129.034501
Mencione a palavra "turbulência" e você pode evocar imagens de vôos acidentados, tempo tempestuoso e correntes oceânicas ou fluviais agitadas. Para muitos, a turbulência é um fato da vida cotidiana, mas também é um dos fenômenos físicos mais mal compreendidos. Em particular, o ponto em que o movimento de um fluido transita de fluxo suave e previsível (conhecido como "laminar") para aleatório e imprevisível (conhecido como "turbulência") - a chamada transição laminar-turbulenta - continua a intrigar os cientistas desde Osborne Reynolds primeiro estudou experimentalmente em tubos em 1883.
Agora, uma equipe de cientistas da Universidade de Illinois Urbana-Champaign, da Universidade da Califórnia em San Diego e da Academia Sinica em Taiwan mostraram como explicar os padrões aleatórios e a dinâmica da turbulência em tubos no regime de transição. Seu trabalho usa idéias novas que se originam em campos tão díspares como mecânica estatística e ecologia e se baseia na crescente evidência de que a transição laminar-turbulenta tem propriedades estatísticas que podem ser melhor pensadas em termos da teoria das transições de fase fora do equilíbrio.
A equipe é composta pelo estudante de pós-graduação em física da UIUC, Xueying Wang, pelo pesquisador da Academia Sinica Hong-Yan Shih e pelo professor emérito de física e pesquisador da UIUC Swanlund, Nigel Goldenfeld. Goldenfeld é atualmente o Distinguished Professor de Física dos Chanceleres da Universidade da Califórnia em San Diego.
Os autores publicaram seus resultados em 11 de julho de 2022, na revista
Physical Review Letters .
Puffs e slugs são características da turbulência transicional Reynolds descobriu que, em tubulações, a transição laminar-turbulenta ocorre de maneira irregular à medida que a velocidade do fluxo aumenta. Bolhas de fluido turbulento, conhecidas hoje como "puffs", aparecem perto da transição laminar-turbulenta e são separadas por regiões de fluxo laminar. As maneiras precisas em que os puffs aparecem e se movem ou mesmo se dividem em dois dependem da geometria do espaço através do qual um fluido flui. Esses fenômenos complexos contribuem para a merecida reputação da turbulência como um dos últimos problemas pendentes da física clássica. Em velocidades ainda mais altas, as manchas turbulentas realmente crescem em vez de apenas se moverem ou se dividirem:essas regiões crescentes de turbulência são chamadas de "lesmas".
Para construir uma imagem mais clara da transição para a turbulência, os pesquisadores desenvolveram um novo modelo mínimo para entender puffs e slugs usando métodos importados da biologia populacional teórica. Os pesquisadores descobriram que eles poderiam representar o fluxo de energia do fluido próximo à transição laminar-turbulenta em termos do fluxo de energia que surge em um ecossistema predador-presa, no qual os nutrientes são a energia do fluxo de fundo, o predador é uma certa estrutura de fluxo que inibe a turbulência, e a turbulência é a presa. Este modelo ecológico recapitula o comportamento turbulento tanto no tubo quanto no fluxo Taylor-Couette, um tipo de fluxo rotacional – um objetivo que os modelos anteriores não conseguiram alcançar.
Goldenfeld diz:"Seis anos atrás, um avanço foi feito com evidências teóricas e experimentais convergindo para uma descrição de sopros turbulentos emergindo de fluxo laminar, em termos de teoria de transição de fase. No entanto, esse trabalho deixou em aberto a questão do que acontece em fluxo mais alto velocidades para longe do ponto de inflexão em si.
"Nosso novo trabalho mostra que a mesma estrutura conceitual e métodos também se aplicam ao regime slug e recapitulam em detalhes notáveis as descobertas experimentais. É fantástico ver conceitos da teoria da transição de fase e da ecologia se unirem no problema completamente diferente da mecânica dos fluidos. "
Os próprios slugs exibem comportamentos interessantes e vêm em dois sabores, slugs fracos e slugs fortes, ambos caracterizados por pelo menos uma "frente", uma região que contém um limite entre fluidos laminar e turbulento.
O autor principal Wang explica:"A frente de uma lesma é como uma frente meteorológica. De um lado da frente está o fluido laminar. Do outro lado está a turbulência. A frente é como um limite de fase e se move no espaço em uma velocidade constante. Em tubulações, você obtém slugs e puffs. Mas slugs fracos em velocidades de fluido mais baixas têm apenas uma frente a montante, enquanto slugs fortes em velocidades mais altas têm frentes nas direções a montante e a jusante. Esses fatores e a riqueza dos fenômenos de transição tornam entender a turbulência transicional é muito difícil. Nosso trabalho fornece uma estrutura unificada que lida com todos esses regimes, diferentes geometrias de fluxo e a aleatoriedade inerente."
Modelos predador-presa e turbulência convergem Os pesquisadores conseguiram tirar proveito de uma conexão surpreendente que encontraram em trabalhos anteriores entre biologia populacional e turbulência transicional.
Modelar como os predadores interagem com suas presas é um tema popular na biologia populacional. A ideia básica é simples:os predadores se reproduzem e comem as presas, reduzindo sua população; as presas também se reproduzem, restaurando seus números e fornecendo comida aos predadores. Então o ciclo se repete. Simplificando, os predadores inibem as presas, enquanto as presas reforçam os predadores. Os cientistas podem deduzir muitas informações desses modelos, como como as populações de predadores e presas variam ao longo do tempo, bem como quanto tempo leva para cada um morrer causado por, digamos, falta de comida ou predação excessiva.
Em um estudo anterior, Shih e Goldenfeld, trabalhando com o ex-graduando Tsung-Lin Hsieh (agora pós-doutorando na Universidade de Princeton), mostraram que existe uma analogia entre modelos predador-presa e turbulência que pode ser expressa em termos matemáticos. Quando o fluido flui através de um tubo, dois tipos de movimento do fluido são gerados. O primeiro tipo é um padrão de vórtice girando em torno do eixo do tubo, chamado de "fluxo zonal". O segundo tipo é a turbulência ao longo do eixo do tubo. Os autores descobriram que a turbulência se acumula de forma constante e ativa o fluxo zonal, que posteriormente suprime a turbulência. Em outras palavras, o fluxo zonal corresponde aos predadores e a turbulência corresponde às presas.
Os pesquisadores descobriram que a distribuição de probabilidade do tempo de vida da turbulência transicional correspondia precisamente à de predadores e presas em um ecossistema, uma conexão impressionante, considerando que a biologia populacional e a dinâmica de fluidos são campos aparentemente díspares.
Hong-Yan Shih comments, "This connection helps us understand the complex transitional behavior of turbulence from the point of view of phase transitions in statistical mechanics. Specifically, this discovery provides the key ingredients to construct an effective theory, which leads to the prediction that the laminar-turbulent transition in fluids is a non-equilibrium phase transition in the directed percolation universality class.
"Directed percolation can be thought of as the familiar process that happens when water drips through coffee grounds in a percolator. If the grounds are too tightly packed, water can't get through. On the other hand, if the grounds are too loosely packed, water can get through but the coffee is undrinkable. There's a critical point where the water just manages to get through and takes long enough so that the coffee tastes good.
"Mathematically, that phenomenon is exactly what happens in the transition to turbulence and the transition of a functioning ecosystem. The mathematics of phase transitions, founded in the Nobel Prize–winning work of K. Wilson, explains how this remarkable phenomenon arises."
This prior work, however, looked at the turbulence of a single puff. Real life isn't as simple, and real fluids near the laminar-turbulent transition contain multiple puffs that grow, die out, and interact in complex ways as the flow speed increases. The researchers needed to extend their model to capture more complicated dynamics beyond those of a single puff.
Extending the predator-prey model by incorporating nutrients To capture the complex dynamics found in experiments beyond the critical point in the current study, the authors decided to take into account energy balance in pipe flow.
Wang explains, "Turbulence is a dissipative structure that needs constant energy input to be sustained, and that energy comes from the laminar flow. This fact was previously shown by exact computer simulations of the fluid equations, but did not allow us to understand in a predictive way the phenomena that would emerge."
The researchers realized that, just like zonal flow and turbulence require energy to persist, predators and prey need nutrients from their environment to survive.
"We wanted to make a minimal model of the full energy balance to extend the previous work and capture energy extraction of turbulence from laminar mean flow," Wang adds. "So we introduced another component into the 'ecosystem':nutrients, which represent the kinetic energy of the mean flow."
The researchers numerically simulated the extended predator-prey model on a two-dimensional lattice having a length much larger than its width. They watched what happens when nutrients—that is, laminar state energy, from the fluid dynamics perspective—flow into the ecosystem, are consumed by the turbulence, and are restored downstream of the turbulence.
The model maps several pathways for energy and population dynamics. The first pathway takes input energy from the energy budget to turbulent energy, like prey extracting nutrients from their environment. A second pathway takes turbulent energy to zonal flow energy, like predators eating prey.
Once they established these predator-prey-inspired pathways, they sat back and watched computer simulations based on the new model, wherein energy entered the pipe and passed through the pathways randomly. Out of the randomness emerged features of transitional turbulence such as puffs, slugs, and their associated fronts, reproducing results seen in experiments. The simulations showed that the appearance of puffs or slugs—and whether slugs are of the weak or strong type—is determined by the input energy (or equivalently, the speed) of the fluid flow.
The researchers then successfully reproduced all the transitional phenomena observed in pipe flow experiments and explained the underlying physics of puff splitting and growth. Specifically, they found that puff splitting and interaction is highly probabilistic. As the fluid speed increases, the probability of puff splitting also increases. The puff-slug transition is gradual, and it occurs when puffs split so frequently that they start to fill up the system densely.
Rotational flow and new questions for turbulence In addition to pipe flow, the researchers also simulated a special type of rotational flow known as Taylor-Couette flow in which a fluid moves in the space between two concentric cylinders and the outer cylinder rotates relative to the inner one. Unlike pipe flow, where the energy enters from the high-pressure end of the pipe, Taylor-Couette flow is sustained by shear, the stress that occurs when two boundaries move parallel to one another. The new model easily incorporated this difference and reproduced the patterns of transitional turbulence seen in experiments, demonstrating the flexibility of the model.
"We showed that the rich and complicated dynamical features in transitional pipe flow can be understood with a simple three-level stochastic predator-prey model based on energy balance in pipe flow," says Wang. "Our model also works for quasi-one-dimensional Taylor-Couette flow. Since energy balance generally holds in fluid systems, we expect our model to be applicable to systems with more complicated geometries as well."
Having described turbulence broadly by implementing their model in two different geometries, the team is already looking to answer new questions.
Goldenfeld says, "The next challenge is to see if and how our probabilistic model can be extended to two- or three-dimensional flows. This problem has been intensely studied for well over twenty years, with new experimental data starting to appear."
For his part, Goldenfeld is pleased to see diverse techniques converge to solve problems in complementary ways, a beautiful demonstration of how different fields of science can inform each other.
Goldenfeld summarizes, "Our results show how stochastic dynamics, pattern formation, phase transitions, and modeling concepts from diverse fields such as ecology can bring new tools, predictions, and insights into a problem previously considered within the more narrow disciplinary focus of fluid dynamics. It is exciting to see how successful minimal modeling is at capturing complex physical phenomena in a quantitative way."
+ Explorar mais Ecological extinction explains how turbulence dies
