
Realização de campo distante, imagem de super-resolução sem rótulo baseada em ondas evanescentes excitadas por mistura não linear de quatro ondas. Crédito:Zhou et al., doi 10.1117 / 1.AP.3.2.025001
O limite de difração, também conhecido como limite de difração de Abbe em óptica, representa um grande desafio em muitos sistemas que envolvem dinâmica de ondas, como imagem, astronomia, e fotolitografia. Por exemplo, o melhor microscópio óptico possui resolução em torno de 200 nm, mas o tamanho físico do processo de fotolitografia com um excimer laser é de cerca de dezenas de nanômetros. Enquanto isso, tamanhos físicos em pesquisas e aplicações atuais em biologia e na indústria de semicondutores foram reduzidos a vários nanômetros, que está muito além da capacidade das ondas ópticas.
De acordo com a teoria do Abade, características de comprimento de onda são geralmente associadas a ondas evanescentes, que decai exponencialmente com a distância do alvo. Em resposta a este problema, pesquisadores desenvolveram muitas maneiras de contornar o limite de Abbe, mostrando sucesso em diferentes aplicações. Em uma instância, o Prêmio Nobel de Química de 2014 foi concedido a Eric Betzig, Stefan W. Hell, e William E. Moerner, por suas contribuições para o desenvolvimento de microscopia de fluorescência super-resolvida para pesquisas em ciências da vida.
Atualmente, Existem duas abordagens principais para superar o limite de difração em óptica:campo próximo e campo distante. A abordagem de campo próximo utiliza uma varredura de ponta nanométrica sobre a amostra e interage diretamente com esses campos evanescentes. Como uma abordagem de digitalização, ele fornece imagens de alta fidelidade, mas é sempre demorado. Por outro lado, abordagens de campo distante, como microscopia de depleção de emissão estimulada (STED), microscopia de reconstrução óptica estocástica (STORM), e microscopia de iluminação estruturada (SIM), são baseados em rotulagem fluorescente, restringindo-os de aplicativos mais amplos, por exemplo, na indústria de semicondutores. É necessária uma abordagem mais fundamental - uma que esteja livre de varredura de campo próximo e nanofabricação, bem como de fluoróforos.
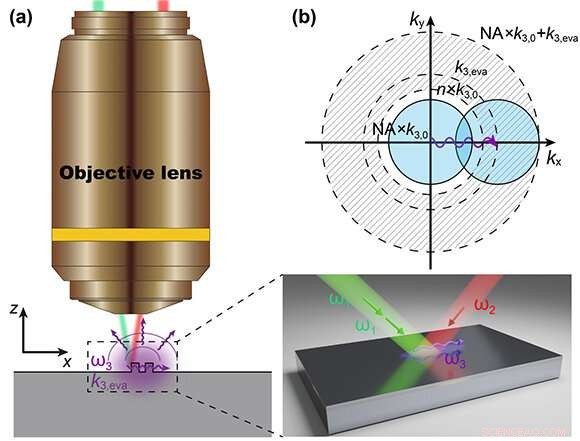
Princípio de funcionamento da imagem de super-resolução de campo distante com base em ondas evanescentes excitadas não linearmente. (a) Esquema do processo de imagem de super-resolução de campo distante com iluminação de onda evanescente localizada excitada pelo processo FWM na interface. A inserção ampliada mostra que o processo FWM ocorre na interface do meio não linear (b) Mecanismo ilustrado no espaço de Fourier. Crédito:Z. Zhao et al., doi 10.1117 / 1.AP.3.2.025001
Uma equipe de pesquisadores da Universidade Jiao Tong de Xangai desenvolveu recentemente uma maneira alternativa de quebrar o limite de difração de Abbe e realizar imagens em comprimentos de onda de uma maneira totalmente óptica. Conforme relatado em Fotônica Avançada , eles propõem iluminações de ondas evanescentes localizadas, que são excitados na superfície do silício por mistura de quatro ondas, um processo óptico não linear de terceira ordem. Essas ondas excitadas ajudam a realizar a super-resolução pela maneira como espalham parte dos campos evanescentes do alvo no campo distante. Por meio da variação de vetores de ondas de ondas excitadas, partes de diferentes orientações no espectro de Fourier podem então ser obtidas. Combinado com uma técnica de reconstrução iterativa chamada de pticografia de Fourier, essas várias partes do espectro de Fourier podem ser empilhadas juntas, recuperar um espectro de Fourier ampliado que inclui campos evanescentes - realizando assim imagens de super-resolução no campo distante.
Sondando as ondas evanescentes em torno de um alvo, a equipe percebe o livre de rótulos, imagem sem varredura de comprimento de onda inferior no campo distante. Os autores observam que seus resultados também são promissores para um novo tipo de mecanismo de fotolitografia de alta resolução:a interferência construtiva de tais ondas evanescentes de campo próximo excitadas pode focar a luz em pequenos pontos bem abaixo do limite de difração.