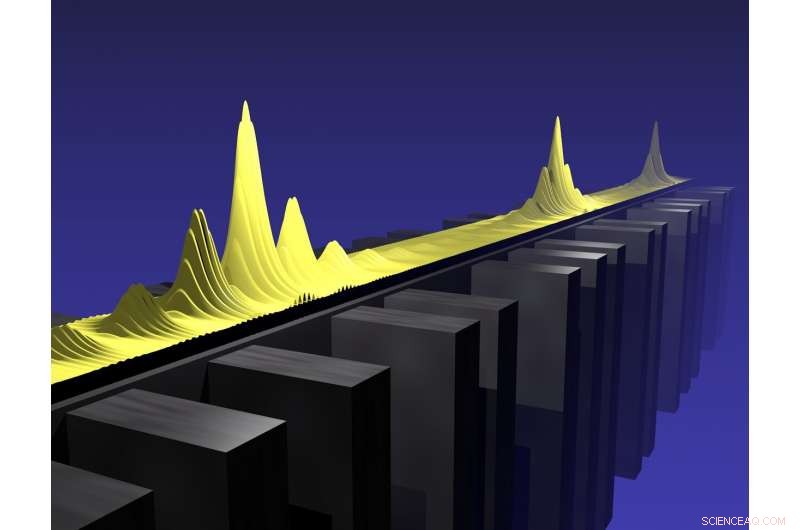
Um estado crítico da padronização quasiperiódica de uma cavidade polariton de semicondutores. Crédito:Aalto University, Jose Lado
O trabalho teórico e experimental combinado resultou em um novo mecanismo por meio do qual a criticidade emerge em estruturas quase-periódicas - uma descoberta que fornece uma visão única da física no meio termo entre ordem e desordem.
Estruturas quasiperiódicas, que são ordenados, mas não são estritamente periódicos, são uma fonte de extraordinária beleza na natureza, arte e ciência. Para físicos, a ordem quase periódica é estética e intelectualmente atraente. Numerosos processos físicos que são bem descritos em estruturas periódicas mudam fundamentalmente seu caráter quando acontecem em sistemas quase-periódicos. Adicione a mecânica quântica, e novos fenômenos surpreendentes podem surgir que permanecem não totalmente compreendidos. Escrevendo em Física da Natureza , uma equipe internacional liderada por Oded Zilberberg do Instituto de Física Teórica da ETH de Zurique e pelos pesquisadores de física do CNRS Jacqueline Bloch da Université Paris-Saclay e Alberto Amo da Lille University, agora descreve o trabalho teórico e experimental combinado no qual eles estabelecem ferramentas versáteis para explorar o comportamento dos sistemas quânticos em uma gama diversificada de configurações quasi-periódicas unidimensionais - e demonstra a força de sua abordagem para descobrir novos mecanismos físicos.
Beleza intrincada
A essência, e beleza, de estruturas quasiperiódicas podem ser apreendidas considerando as placas de piso. Um piso pode ser facilmente revestido com ladrilhos sem lacunas usando peças idênticas de, por exemplo, triangular, forma quadrada ou hexagonal, repetindo um padrão simples. Mas uma superfície plana também pode ser totalmente coberta por padrões não repetitivos, e que usando apenas dois tipos de ladrilhos romboides, como o físico e matemático inglês Roger Penrose ficou famoso (veja a figura). Nesse caso, mesmo que as configurações locais apareçam em lugares diferentes, o padrão geral não pode ser sobreposto a si mesmo por translação e rotação. Como tal, esses sistemas ocupam uma espécie de meio termo entre as estruturas periódicas e aleatoriamente desordenadas.
Nesse meio-termo, há física intrigante a ser explorada. Pegue um cristal perfeitamente ordenado. Lá, a periodicidade permite a propagação ondulatória de elétrons através do material, por exemplo, em um metal. Se a perfeição cristalina é perturbada pela introdução de desordem, o comportamento muda. Para baixos níveis de desordem, o material ainda conduz, mas menos bem. Em algum nível de desordem, os elétrons param de se propagar e se tornam coletivamente localizados, em um processo conhecido como localização de Anderson. Para redes periódicas, este efeito foi descrito pela primeira vez em 1958 (por Philip Anderson, ganhador do Nobel de Física em 1977, que faleceu em 29 de março deste ano). Mas a forma como esses processos atuam em estruturas quase-periódicas continua a ser uma área de pesquisa ativa.
Interpolação perspicaz
Uma ampla gama de fenômenos físicos não convencionais foi descrita para sistemas quase-periódicos, mas não existe uma estrutura abrangente para lidar com a propagação de ondas em estruturas quase-periódicas. Existem, Contudo, vários modelos que permitem estudar aspectos específicos do transporte e da localização. Dois exemplos paradigmáticos de tais modelos são os modelos Aubry-André e Fibonacci, cada um dos quais descreve diferentes fenômenos físicos, principalmente quando se trata de propriedades de localização.
No modelo Aubry-André, existem duas regiões de parâmetros distintas nas quais as partículas podem estar em estados 'estendidos' ou localizados (no mesmo sentido em que os elétrons podem se propagar através de um material ou ficar presos em um estado de isolamento). Por contraste, no modelo de Fibonacci não há um ponto crítico específico separando os dois regimes, mas para qualquer parâmetro, o sistema está em um estado crítico entre localizado e estendido. Apesar de seus comportamentos nitidamente contrastantes, os dois modelos estão conectados um ao outro, e um pode ser continuamente transformado no outro. Isso é algo Zilberberg, então trabalhando no Instituto Weizmann de Ciência em Israel, havia demonstrado em um trabalho inovador com seu colega Yaacov Kraus em 2012. A questão que permanecia era como os dois comportamentos de localização tão diferentes estão conectados.

O trabalho teórico e experimental combinado revela um novo mecanismo através do qual a criticidade emerge em estruturas quase-periódicas - uma descoberta que fornece uma visão única da física no meio termo entre ordem e desordem. Crédito:ETH Zurich / D-PHYS Oded Zilberberg
Acumulando novos insights
Para responder a essa pergunta, Zilberberg com seu Ph.D. o estudante Antonio Štrkalj e seu ex-pós-doutorado Jose Lado (agora na Aalto University) se uniram aos experimentalistas do CNRS Jacqueline Bloch e Alberto Amo e seu Ph.D. aluno Valentin Goblot (agora na empresa STMicroelectronics). Os físicos franceses haviam aperfeiçoado uma plataforma fotônica - a chamada rede de cavidade-polariton - na qual a luz pode ser guiada através de nanoestruturas semicondutoras enquanto experimenta interações semelhantes às que atuam nos elétrons que se movem através de um cristal. Mais importante, eles encontraram maneiras de gerar modulações quase-periódicas em seus fios fotônicos que lhes permitiram implementar experimentalmente, pela primeira vez em qualquer sistema, o modelo Kraus-Zilberberg. Os experimentos de espectroscopia óptica realizados localmente nesses quase-cristais fotônicos oferecem a possibilidade requintada de obter imagens diretamente da localização da luz nos sistemas.
Ao combinar suas ferramentas teóricas e experimentais, os pesquisadores foram capazes de rastrear como o modelo de Aubry-André evolui para se tornar totalmente crítico no limite do modelo de Fibonacci. Expectativa contra ingênua, a equipe mostrou que isso não acontece de maneira suave, mas através de uma cascata de transições localização-deslocalização. Iniciando, por exemplo, da região do modelo Aubry-André onde as partículas estão localizadas, em cada etapa das bandas de energia do processo em cascata se fundem em uma transição de fase, durante o qual as partículas estão passando pelo material. Do outro lado da transição em cascata, a localização praticamente dobra, enviando os estados do modelo de Aubry-André gradualmente em direção à criticidade total à medida que se transforma no modelo de Fibonacci.
A situação tem alguma semelhança com o que acontece com uma pilha de arroz quando os grãos são adicionados um a um. Por algum tempo, grãos recém-adicionados ficarão apenas onde pousaram. Mas, uma vez que a inclinação no local de pouso excede uma inclinação crítica, uma avalanche local é induzida, levando a um rearranjo de partes da superfície da pilha. A repetição do processo eventualmente leva a uma pilha estacionária onde um grão adicional pode desencadear uma avalanche em qualquer uma das escalas de tamanho relevantes - um estado 'crítico'. Nos sistemas quase-periódicos, a situação é mais complexa por causa da natureza quântica das partículas envolvidas, o que significa que eles não se movem como partículas, mas interfere como as ondas fazem. Mas também neste cenário, a evolução para um estado crítico geral acontece, como na pilha de arroz, através de uma cascata de transições discretas.
Com a descrição teórica e observação experimental desta cascata para a criticidade, as equipes conectaram com sucesso fenômenos quânticos em dois modelos paradigmáticos de cadeias quasi-periódicas, adicionando uma visão única sobre o surgimento de criticidade. Além disso, eles desenvolveram uma plataforma experimental flexível para futuras explorações. A importância desses experimentos vai além das propriedades da luz. O comportamento dos elétrons, átomos e outras entidades quânticas são governados pela mesma física, que poderia inspirar novas formas de controle quântico em dispositivos. Assim como o apelo de padrões quase-periódicos transcende as disciplinas, o potencial para inspirar avanços científicos e, eventualmente, tecnológicos parece igualmente ilimitado.