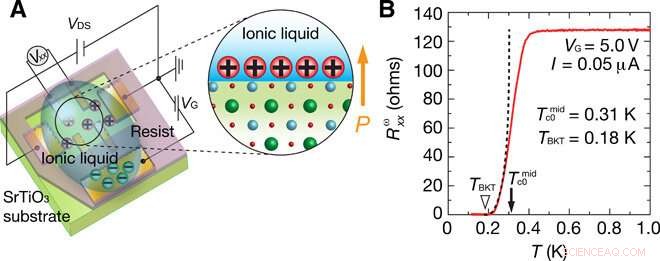
Imagem do dispositivo e supercondutividade induzida pela porta em SrTiO3. (A) Imagem esquemática de SrTiO3-EDLT. (B) Resistência longitudinal do primeiro harmônico Rωxx em função da temperatura T sob campo magnético zero. A corrente aplicada foi de 0,05 μA, que pode ser considerado como limite de baixa corrente. A temperatura de transição definida pelo ponto médio da transição resistiva é estimada como Tc0 =0,31 K (seta preta). A linha tracejada preta mostra a curva de ajuste pela fórmula de Halperin-Nelson, onde RN =128 ohms é a resistência de estado normal (T =1,0 K), b =1,17 é uma constante adimensional, e TBKT =0,18 K é a temperatura de transição BKT (triângulo branco). A tensão de porta aplicada VG é 5,0 V em T =260 K. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Na ciência dos materiais, sistemas de elétrons bidimensionais (2DES) realizados na superfície ou interface do óxido são um candidato promissor para alcançar novas propriedades físicas e funcionalidades em um campo quântico emergente rapidamente. Enquanto o 2-DES fornece uma plataforma importante para eventos quânticos exóticos, incluindo o efeito Hall quântico e supercondutividade, o efeito da quebra de simetria; transição de um estado desordenado para um estado mais definido, em tais fases quânticas permanecem indescritíveis. O transporte elétrico não recíproco ou a resistência dependente da direção da corrente é uma sonda para simetria de inversão quebrada (presença de um dipolo), como observado em vários cristais não centrossimétricos e interfaces. Em um novo relatório, Yuki M. Itahashi e uma equipe de cientistas em física aplicada, nanossistemas e ciência de materiais no Japão e nos EUA relataram transporte não recíproco na superfície de um supercondutor 2-D feito de titanato de estrôncio material supercondutor (SrTiO 3 ) A equipe observou um aumento gigantesco da região não recíproca na região de flutuação supercondutora - seis ordens de magnitude maior em comparação com seu estado normal. Os resultados agora são publicados em Avanços da Ciência e demonstrar características sem precedentes do supercondutor polar 2-D.
Condutores polares ou supercondutores são plataformas de materiais potenciais para transporte quântico e funcionalidades spintrônicas, com transporte não recíproco inerente que reflete a propriedade indescritível de quebra de simetria de reversão de tempo (isto é, quebra de conservação de entropia). Experimentos recentes se estenderam ao estado supercondutor para observar uma grande resposta não recíproca e os físicos estão ansiosos para examinar a não reciprocidade em torno da transição supercondutora em um sistema eletrônico simples. Por esta, Itahashi et al. eletrodos de cromo / ouro (Cr / Au) projetados na superfície atomicamente plana de SrTiO 3 e colocado líquido iônico no topo para formar um transistor elétrico de camada dupla (EDLT) para realizar um supercondutor Rashba; com base no efeito Rashba, com uma técnica de ionização no SrTiO 3 superfície do material. Os cientistas então mediram o primeiro e o segundo transporte eletrônico harmônico usando uma técnica de bloqueio padrão para medir o transporte de carga não recíproca e quantificar a quebra de simetria de reversão de tempo no sistema. O transporte não recíproco também é uma ferramenta eficaz para identificar pares de Cooper, onde um par de elétrons supera sua repulsão usual para compartilhar um estado quântico de paracondutividade não recíproca em supercondutores, que Itahashi et al. também pretende quantificar no supercondutor Rashba.
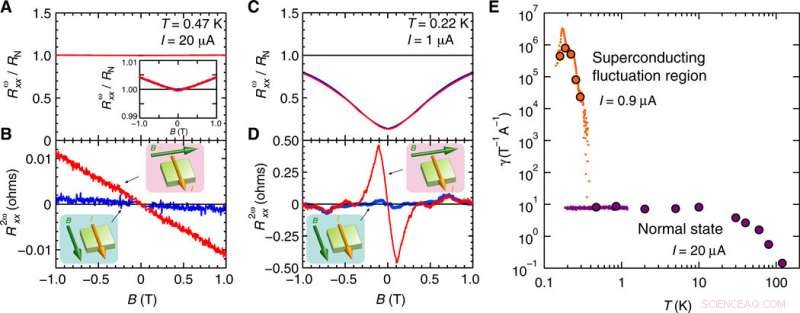
Magnetotransporte de SrTiO3 2D induzido por porta para os estados normal e supercondutor e aumento do transporte não recíproco na região de flutuação supercondutora. (A) Primeiro e (B) segundo magnetorresistência harmônica (Rωxx e R2ωxx, respectivamente) acima de Tc0 (estado normal, T =0,47 K e I =20 μA) em função do campo magnético no plano B perpendicular (vermelho) ou paralelo (azul) a I. As inserções em (A) e (B) mostram a visão ampliada de Rωxx (B) e esquemas da configuração de medição (direções de B e I), respectivamente. (C) Rωxx e (D) R2ωxx abaixo de Tc0 (região de flutuação supercondutora, T =0,22 K e I =1 μA) em função do plano B perpendicular (vermelho) ou paralelo (azul) a I. Em (A) a (D), Rωxx é normalizado pela resistência de estado normal RN =128 ohms, e Rωxx / R2ωxx é simetrizado / anti-simetrizado em função de B. (E) Dependência de γ =2R2ωxxRωxxBI no estado normal (I =20 μA) e região de flutuação supercondutora (I =0,9 μA). Círculos roxo (estado normal) e laranja (região de flutuação supercondutora) foram extraídos da medição da varredura do campo magnético de R2ωxx em B baixo abaixo de 0,1 T, enquanto os pontos roxos (estado normal) e laranja (região de flutuação supercondutora) foram plotados a partir da varredura de temperatura de R2ωxx sob B =3 e 0,05 T, respectivamente. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Os cientistas inicialmente detalharam a primeira resistência harmônica (FHR) correspondente à resistência linear próxima à transição supercondutora para uma tensão de porta de 5,0 V. Os resultados mostraram uma dependência da temperatura no limite de corrente baixa (I =0,05 μA). Em seguida, eles se concentraram na resistência de segundo harmônico (SHR) e no transporte de carga não recíproco creditado observado na superfície de SrTiO 3 à simetria polar dentro da região de flutuação supercondutora e no estado normal. A equipe observou o transporte de magneto em SrTiO 2-D induzido por portão 3 dentro de um campo magnético (B) perpendicular à corrente (I) para estados normais e supercondutores - com transporte não recíproco aprimorado na região de flutuação supercondutora. Para comparar a magnitude da não reciprocidade entre o estado normal e a região de flutuação da supercondutividade, eles calcularam o coeficiente de magnetorresistência não recíproca (γ), que dependia da temperatura dentro das regiões.
A equipe posteriormente mediu a dependência dos sinais do segundo harmônico na corrente (I), no estado normal e na região de flutuação supercondutora. No estado normal, o SHR mostrou uma dependência quase linear da corrente. Na região de flutuação da supercondutividade em um campo magnético de 0,1 Tesla, o SHR aumentou linearmente, atingiu um máximo em torno de 1 µA e suprimido - para indicar a supressão da supercondutividade pela alta corrente.
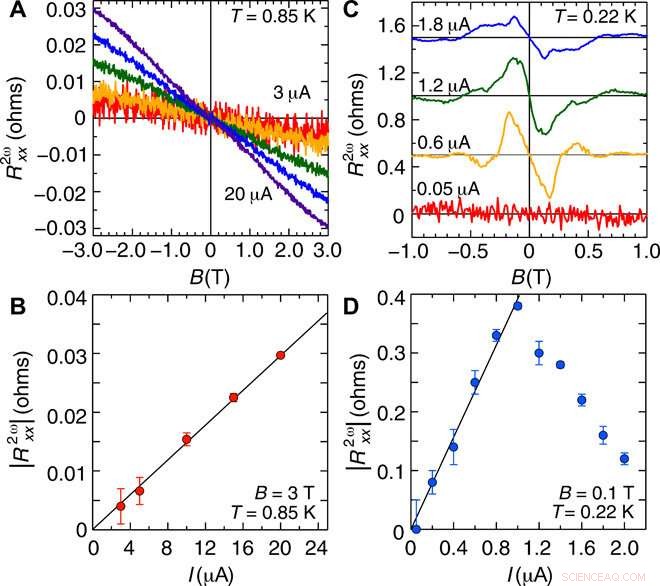
Dependência da corrente da magnetorresistência do segundo harmônico na região normal e na região de flutuação supercondutora. (A) Magnetoresistência do segundo harmônico R2ωxx em T =0,85 K sob I =3 μA (vermelho), 5 μA (laranja), 10 μA (verde), 15 μA (azul), e 20 μA (roxo). R2ωxx é antissimetrizado em função de B. (B) ∣∣R2ωxx∣∣ em B =3 T como função de I, que é extraído de (A). A linha sólida preta mostra o ajuste linear como uma função de I. (C) Dependência do campo magnético de ∣∣R2ωxx∣∣ em T =0,22 K em I =0,05 μA (vermelho), 0,6 μA (laranja), 1,2 μA (verde), e 1,8 μA (azul). Cada curva é deslocada verticalmente em 0,5 ohms e anti-simetrizada em função de B. (D) Dependência de corrente de ∣∣R2ωxx∣∣ em B =0,1 T, onde R2ωxx é considerado uma função linear de B. Na região de baixa corrente (I ≤ 1 μA), ∣∣R2ωxx∣∣ aumenta linearmente (linha sólida preta) com I. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Para investigar mais a fundo a possível origem do transporte supercondutor não recíproco no sistema, os cientistas mediram a dependência da temperatura de FHR e SHR durante a transição. Para conseguir isso, eles notaram a dependência do campo magnético de FHR e SHR em várias temperaturas e observaram especificamente que SHR é amplamente aprimorado durante o transporte supercondutor. Embora Itahashi et al. aplicou uma corrente relativamente grande e um campo magnético no plano, eles registraram o estado de resistência zero na temperatura mais baixa. Os resultados implicaram na existência da transição Berenzinskii-Kosterlitz-Thouless (transição BKT), nomeado após uma equipe de físicos de matéria condensada ganhadores do prêmio Nobel. Ele descreve as transições de fase em sistemas 2-D na física da matéria condensada aproximadas por um modelo XY, a fim de compreender fases ou estados incomuns da matéria em supercondutores.
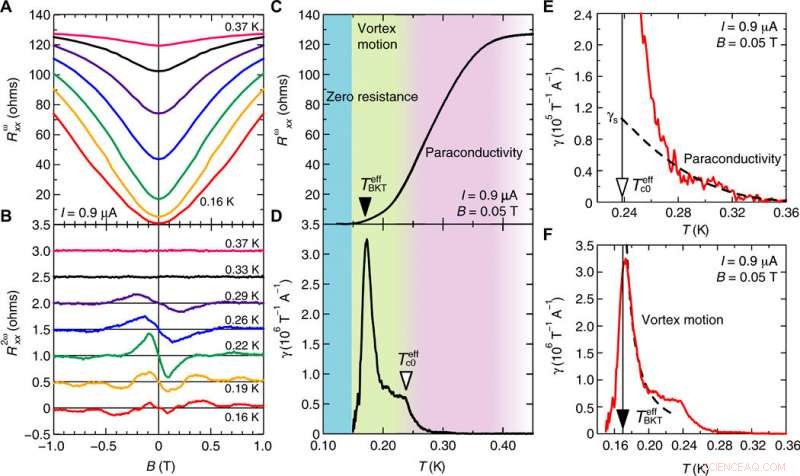
Dependência da magnetorresistência e do transporte não recíproco com a temperatura. Dependência do campo magnético de (A) o primeiro (Rωxx) e (B) o segundo (R2ωxx) magnetorresistência harmônica em T =0,16 K (vermelho), 0,19 K (laranja), 0,22 K (verde), 0,26 K (azul), 0,29 K (roxo), 0,33 K (preto), e 0,37 K (rosa), respectivamente. Em B), cada curva é deslocada verticalmente em 0,5 ohms. Rωxx / R2ωxx é simetrizado / antissimetrizado em função de B. Variação de temperatura de (C) Rωxx e (D) γ em B =0,05 T e I =0,9 μA. Nessa região, R2ωxx é linear em função de B e I. Rωxx / γ é simetrizado / antissimetrizado em função de B. Estrutura característica (estrutura de torção em torno de T =0,24 K e estrutura de pico em torno de T =0,17 K) aparece em (D), segundo o qual podemos identificar duas regiões do transporte não recíproco de origens diferentes, ou seja, região de paracondutividade e região de vórtice. Na temperatura mais baixa, estado de resistência zero é observado, onde Rωxx e γ tornam-se insignificantemente pequenos. Ampliação de γ na região de paracondutividade (E) e região de vórtice (F). A linha tracejada preta em (E) mostra a curva de ajuste por γ (T) =γs (1 − R (T) RN) 2, e a linha tracejada preta em (F) indica curva de ajuste por γ (T) =C (T − TeffBKT) −3/2. A resistência de estado normal RN =128 ohms é definida como Rωxx em T =1,0 K. Crédito:Science Advances, doi:10.1126 / sciadv.aay9120
Desta maneira, Yuki M. Itahashi e colegas propuseram o transporte não recíproco em supercondutores 2-D não centrossimétricos (sem simetria de inversão) dentro de um campo magnético. O transporte não recíproco originou-se da flutuação da amplitude do estado normal para o supercondutor. A dependência com a temperatura do coeficiente de magnetorresistência não recíproca (γ) observada nos experimentos concordou bem com o quadro teórico microscópico de movimento livre para vórtices termicamente excitados e antivórtices em supercondutores polares 2-D. A resposta não recíproca é, portanto, uma ferramenta poderosa para entender a natureza dos supercondutores não centrossimétricos.
Itahashi et al. acreditam que o transporte não recíproco pode aparecer universalmente para diferentes materiais em sistemas supercondutores interfaciais com simetria polar. Os resultados fornecem informações sobre funções de supercondutividade até então desconhecidas e informações importantes sobre o estado eletrônico e mecanismos de emparelhamento em supercondutores não centrossimétricos - como um tópico importante para investigação futura. O trabalho destacou o transporte não recíproco em sistemas supercondutores interfaciais, como o supercondutor 2-D induzido por porta SrTiO 3 . A equipe investigou o salto acentuado do transporte não recíproco do estado normal para o supercondutor como evidência direta do aumento gigante do transporte não recíproco no sistema. Os resultados oferecem uma visão importante dos supercondutores polares e abrem uma nova maneira de pesquisar propriedades e funcionalidades emergentes até então desconhecidas em interfaces de óxido 2-D e supercondutores.
© 2020 Science X Network