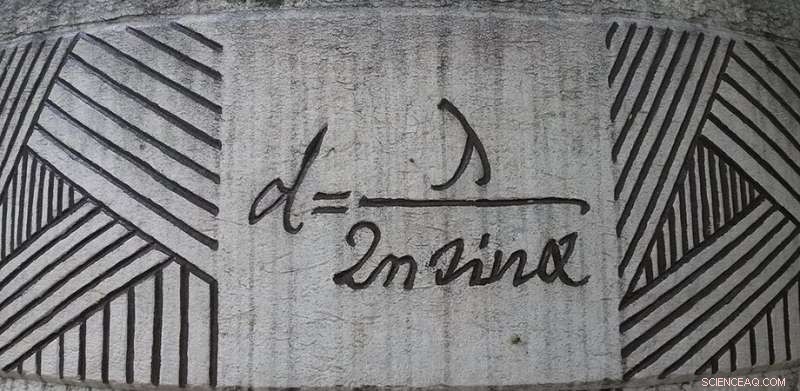
Equação de difração de Ernst Abbe em exibição em Jena, Alemanha. Crédito:Daniel Mietchen, Wikimedia, commons.wikimedia.org/wiki/File:Ernst-Abbe-Denkmal_Jena_F%C3%BCrstengraben_-_20140802_125709.jpg
Embora nos digam que uma imagem fala mais que mil palavras, esse clichê subestima seriamente o valor de uma boa imagem. Nossa compreensão de como o mundo funciona é simplificada por nossa capacidade de transformar dados em imagens. A imagem está no cerne da ciência:se pode ser medida, será transformado em uma imagem a ser analisada.
O fator limitante da imagem é a resolução. Quão próximos dois objetos podem estar antes que um sistema de imagem os reduza a um único ponto borrado? Essa pergunta foi inicialmente respondida por Ernst Abbe em 1873. Ele teorizou que se dois objetos estão mais próximos do que cerca de meio comprimento de onda, eles não podem ser resolvidos. Abbe obteve seu limite considerando como a difração por uma lente borraria uma fonte pontual.
Por cerca de um século, O limite de difração de Abbe foi considerado uma verdade científica. Certo, você pode jogar alguns jogos com a luz iluminadora e o meio de imagem para obter um fator de dois ou três, mas fatores de dez ou 100 eram inconcebíveis. Isso agora mudou, com muitas técnicas de imagem capazes de resolver além do limite de difração de Abbe, que agora está despedaçado no canto da oficina da ciência sob a sombra de dois prêmios Nobel. Mas ainda existe um limite? Quão próximos dois objetos podem estar antes de se tornarem desfocados em um único ponto? Esta é a pergunta que Evgenii Narimanov da Purdue University procurou responder em um recente Fotônica Avançada papel.
Imagem de desfibramento
Quando se trata de imagem, é muito mais simples deixar de lado o conceito de difração e pensar, em vez disso, na informação. Quando a imagem de um objeto é criada, a luz é espalhada pelo objeto em direção ao sistema de imagem. O padrão espacial, ou informação, da imagem é transportada pelas frequências espaciais da luz. Para recuperar uma imagem precisa, o sistema de imagem deve transmitir essas frequências espaciais sem modificá-las. Mas, todo sistema tem seus limites, assim, a contribuição de algumas frequências espaciais será perdida.
A imagem resultante é feita pela recombinação das frequências espaciais que são transmitidas pelo sistema de imagem. Se o sistema de imagem não pode transmitir frequências acima de um certo limite, então a imagem não conterá essa informação, resultando em desfoque. Se você considerar o sistema de imagem capaz de transmitir frequências espaciais até uma frequência de corte, mas incapaz de transmitir frequências acima do corte, então a resolução da imagem resultante será exatamente como previsto por Abbe (mas com matemática mais simples).
De fato, a informação transmitida por um sistema de imagem é descrita exatamente pela mesma matemática usada por engenheiros que estudam a transmissão de dados por fios telefônicos, que permite que as ferramentas da teoria da informação sejam usadas para prever o desempenho dos sistemas de imagem.
Decodificando as mensagens em uma imagem
Narimanov deu um passo adiante na abstração do processo de imagem, considerando apenas a transferência de informações, independentemente de como essas informações são codificadas. Quando isso for feito, a resolução de uma imagem é determinada apenas pela informação mútua compartilhada entre o objeto e a imagem. Nesta estrutura, que é independente de todos os detalhes funcionais, o limite de resolução é dado pelo ruído introduzido durante a transferência de informações. Na prática, o ruído é devido ao detector, espalhamento de luz, flutuações nas condições de iluminação, e muitos mais detalhes.
Ao adotar essa abordagem abstrata, Narimanov conseguiu produzir uma teoria que prevê a melhor resolução possível para uma imagem com base apenas na proporção entre a intensidade do sinal e a quantidade de ruído. Quanto maior a relação sinal-ruído, melhor será a resolução possível.
Aproveitando esta teoria, o artigo também inclui uma série de cálculos para sistemas de imagem mais específicos, como aqueles que usam iluminação estruturada, e para o caso de imagens de objetos esparsos, que têm poucos recursos frequentemente agrupados. As possibilidades de melhorar uma imagem com o pós-processamento também são discutidas:todos nós estamos familiarizados com dramas policiais na televisão que parecem capazes de aprimorar imagens à vontade. Embora isso não seja possível conforme mostrado na TV, existe um elemento de verdade. Métodos válidos para pós-processamento computacional de uma imagem podem revelar alguns detalhes ocultos. Esta teoria mostra os limites dessa abordagem, também.
A abordagem de Narimanov não revela qual aspecto de um sistema atualmente limita a resolução. Por isso, modelos mais específicos ainda são necessários. Em vez de, é melhor pensar no modelo de Narimanov como um guia:onde estão os maiores ganhos em resolução a serem encontrados com o mínimo de esforço? Essas informações são úteis para decidir onde investir tempo e dinheiro.