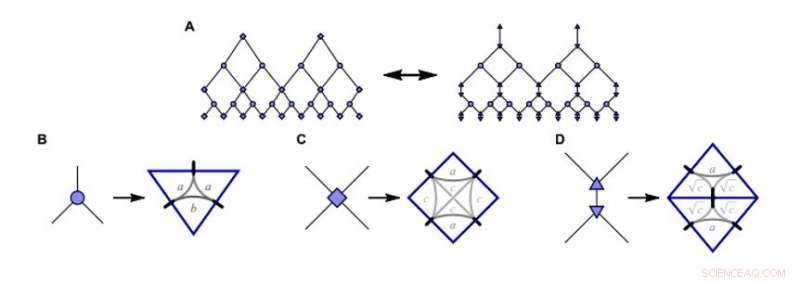
Construindo o modelo de brinquedo do matchgate MERA (multiescala emaranhamento renormalização ansatz; mMERA). A:A rede de tensores MERA padrão (à esquerda) na configuração de matchgate numérica do estudo é equivalente a B-D:Isometries, desenredadores, e desenredadores triangulados (da esquerda para a direita) expressos como tensores matchgate. Os parâmetros livres a, b, c fixa os componentes das matrizes geradoras. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Redes de tensores têm um papel central na física quântica, pois podem fornecer uma aproximação eficiente para classes específicas de estados quânticos. A linguagem gráfica associada também pode facilmente descrever e raciocinar pictoricamente sobre os circuitos quânticos, canais, protocolos e sistemas abertos. Em um estudo recente, A. Jahn e uma equipe de pesquisa nos departamentos de sistemas quânticos complexos, materiais e energia e matemática e ciência da computação na Alemanha introduziram uma estrutura versátil e eficiente para estudar redes de tensores estendendo as ferramentas anteriores. Os pesquisadores usaram o bulk tiling (técnica geométrica de computação) em seu trabalho para obter dados críticos de alta precisão e estabeleceram uma ligação entre os códigos de correção de erros quânticos holográficos e as redes de tensores. Eles esperam que o trabalho estimule investigações adicionais de modelos de rede tensorial para capturar correspondências de fronteira em massa. Os resultados agora são publicados em Avanços da Ciência .
A correspondência AdS / CFT, que significa correspondência anti-de Sitter / teoria de campo conforme, é uma das maiores áreas de pesquisa da teoria das cordas, e é um exemplo no contexto de dualidades de limite em massa em que existe uma dualidade holográfica entre a gravidade em um espaço em massa e um campo quântico crítico em seu limite. Esta correspondência que relaciona duas teorias muito diferentes foi originalmente formulada pelo físico Juan M. Maldacena em 1997, e é considerado um resultado significativamente importante na teoria das cordas nos últimos 20 anos.
Uma característica-chave dessas dualidades é a relação entre a geometria em massa e as entropias de emaranhamento de contorno, que os físicos já haviam esclarecido usando a fórmula Ryu-Takayanagi. Uma vez que é importante entender o emaranhamento no contexto de AdS / CFT, pesquisadores perceberam a necessidade de redes de tensores como uma estrutura ideal para construir modelos de brinquedos holográficos, como a simulação ansatz de renormalização de emaranhamento multiescala (MERA). Os físicos já haviam explorado a compreensão de que a correção de erros quânticos poderia ser facilitada por uma dualidade holográfica, que ainda mais conectado às idéias da teoria da informação quântica. Embora os pesquisadores tenham construído com sucesso vários modelos de rede tensorial para reproduzir uma variedade de aspectos em AdS / CFT, eles ainda não tinham uma compreensão geral das características e limites da holografia da rede tensorial. Obstáculos específicos ao processo incluem os espaços de parâmetros potencialmente grandes de redes de tensores e os consideráveis custos computacionais envolvidos.
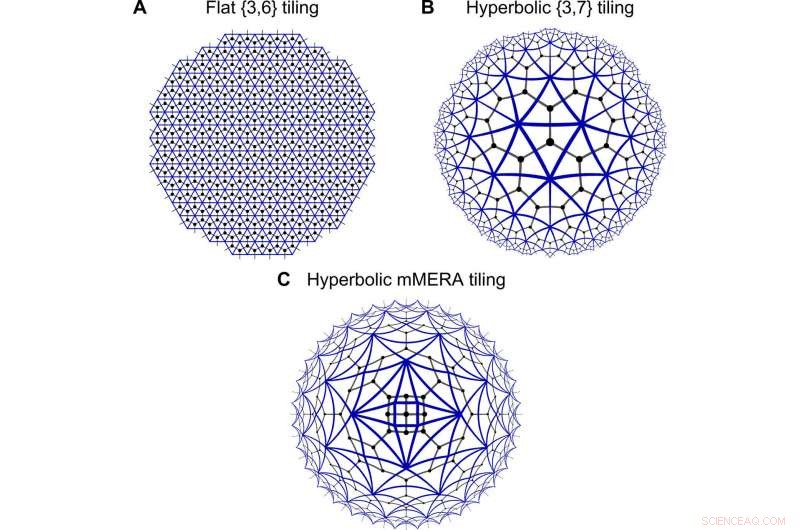
Geometrias de redes tensoras. Discretizações de espaço plano (A) e hiperbólico (B e C) com ladrilhos triangulares (bordas azuis), na qual uma rede de tensores está embutida (rede preta). No formalismo matchgate, arestas de junção entre triângulos correspondem a uma integração sobre um par de números de Grassmann, análogo à contração da rede tensorial sobre os índices. Enquanto (A) e (B) mostram coisas regulares, (C) apresenta um mosaico não regular semelhante a MERA, que os cientistas chamaram de matchgate MERA (mMERA). Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
No presente trabalho, Jahn et al. superou os desafios existentes aplicando técnicas de contração altamente eficientes desenvolvidas por tensores matchgate. As técnicas versáteis permitiram que a equipe de pesquisa estudasse de forma abrangente a interação da geometria e das correlações em redes de tensores fermiônicos gaussianos, incorporando modelos de brinquedo de correção de erros quânticos. Eles também incluíram abordagens de rede de tensores anteriores, como o modelo "MERA 'no presente trabalho, para destacar as conexões entre eles. A equipe restringiu o estudo a redes de tensores não-unitárias e reais, assemelhando-se a uma evolução euclidiana do volume ao limite. Jahn et al. forneceu novas abordagens no contexto da renormalização da rede tensorial, para substanciar a capacidade das redes de tensores de descrever correspondências de limite de volume além dos modelos conhecidos. O presente trabalho é preliminar e fornece um ponto de partida para estudos mais sistemáticos sobre holografia em redes de tensores.
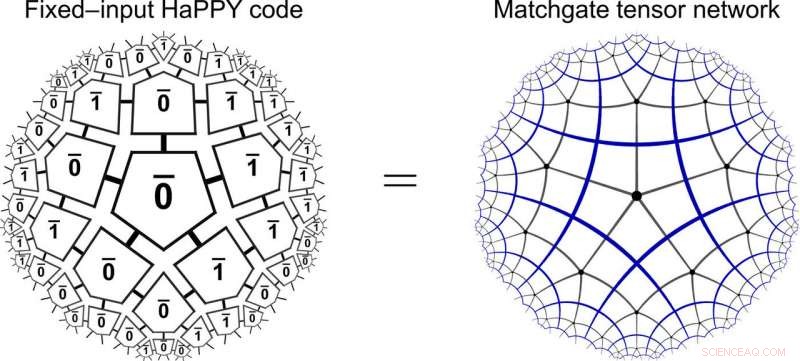
Equivalência HaPPY / matchgate. O código do pentágono holográfico do modelo HaPPY para entrada de massa computacional fixa (à esquerda) é igual a uma rede de tensores de matchgate em uma telha pentagonal hiperbólica (à direita). Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Os cientistas primeiro aplicaram sua estrutura à classe altamente simétrica de telhas regulares para implementar o código de correção de erro holográfico (código HaPPY) proposto em outro lugar. Depois disso, eles exploraram a versatilidade da estrutura para estendê-la para configurações mais físicas. Eles primeiro usaram o modelo de brinquedo de código HaPPY para entender a correspondência em massa / limite com ladrilhos em massa de pentágonos holográficos, onde cada bloco de pentágono codifica um qubit lógico tolerante a falhas. Brevemente, a equipe de pesquisa observou que fixar os graus de liberdade em massa para estados de base computacional poderia dar origem a uma rede de tensores matchgate. Eles mostraram que os estados da base computacional são gaussianos puros e concluíram que, para a entrada computacional fixa na massa, o código do pentagrama holográfico poderia produzir um tensor de matchgate na fronteira. Usando um símbolo Schläfli {p, q} onde p =o número de arestas por polígono e q =o número de polígonos ao redor de cada canto, eles especificaram a geometria hiperbólica do modelo HaPPY.
Depois de Jahn et al. mostraram sua estrutura de modelo para incluir o código do pentágono holográfico construído a partir de estados estabilizadores de cinco qubit para entradas em massa fixas. Eles mostraram que os estados de fronteira correspondem ao emparelhamento não local com partículas exóticas conhecidas como férmions de Majorana. O trabalho, portanto, abriu uma avenida para estudar as propriedades de estado de um modelo holográfico em tamanhos grandes. Os cientistas calcularam ainda os correlacionadores de dois pontos e as entropias de emaranhamento do sistema. Eles então mostraram que os estados limites Gaussianos críticos e com lacunas poderiam ser realizados além dos modelos conhecidos usando várias telhas em massa. No presente trabalho, eles reproduziram as propriedades de escala média do modelo de brinquedo Ising CFT (conformal field theory); modelo mais simples possível em física teórica que permitiu métodos da teoria quântica de campos euclidiana e o estudo de fenômenos críticos.
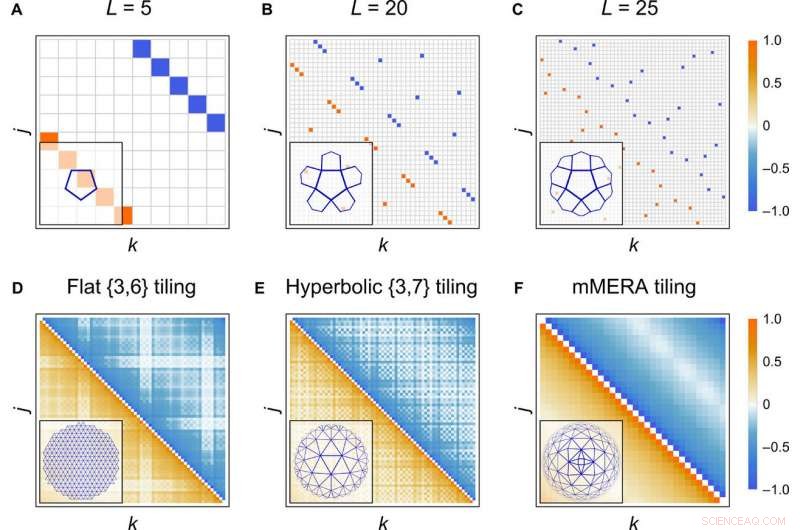
Correlações de estado limite. (A a C) Matriz de covariância de Majorana Γ com entradas codificadas por cores para um estado de fronteira de um {5 hiperbólico, 4} ladrilho do código HaPPY com entrada 0¯ fixa em cada ladrilho. O limite consiste em 2L =10, 40, e 50 sites de Majorana, respectivamente. (D a F) Matriz de correlação de campo 〈ψjψk - ψkψj〉 / 2 =(Γ2j, 2k − 1 + Γ2j − 1, 2k) / 4 para estados limites de {3, 6}, {3, 7}, e mMERA tiling na criticidade com L =63, 69, e 64 locais de fronteira, respectivamente. As entradas da matriz são normalizadas para a mesma escala de cores. O mosaico correspondente a cada matriz de correlação em (A) a (F) é mostrado no canto esquerdo inferior. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
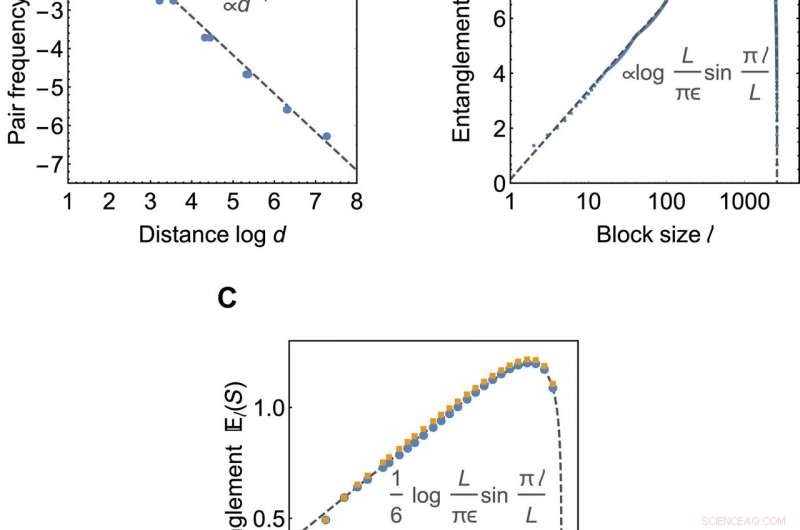
Correlações críticas e escala de emaranhamento. (A e B) Propriedades do estado limite do código HaPPY em 2605 locais limite. (A) mostra correlações médias na distância limite d, calculado como a frequência relativa n de pares de Majorana. A linha cinza tracejada mostra um ajuste numérico n (d) ~ 1 / d. (B) mostra a escala da entropia de emaranhamento média El (S) com o tamanho do subsistema l. A linha cinza tracejada mostra o ajuste numérico usando (11). (C) El (S) para tilings regulares nos valores críticos a =0,580 para a {3, 6} lado a lado (azul) e em a =0,609 para o {3, 7} lado a lado (amarelo) com 348 locais de limite cada. A linha cinza tracejada mostra a solução exata c =1/2 CFT. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Jahn et al. em seguida, construiu uma rede de tensores de matchgate euclidiana baseada na geometria MERA desenvolvida anteriormente e chamou-a de matchgate MERA (mMERA). Esta invariância de mosaico que eles expressaram como uma triangulação (medidas múltiplas para capturar um construto), recuperou o Ising CFT com pouco custo computacional. O processo de otimização computacional no estudo levou apenas alguns minutos em um computador desktop para uma rede com centenas de tensores.
Desta maneira, A. Jahn e colegas introduziram uma estrutura preliminar eficiente para estudar redes de tensores e propuseram estudos adicionais dentro da configuração gaussiana para focar em volumes positivamente curvos, modelos dimensionais superiores e tensores aleatórios. Estudos adicionais além da Gaussianidade poderiam explorar redes de tensores fermiônicos interagentes por expansão de acoplamento fraco ou sob interações restritas localmente. Ambas as possíveis extensões sugeridas do framework apresentadas no estudo irão requerer apenas escalonamento computacional polinomial para o tamanho do sistema para evitar esforços computacionais proibitivos de métodos gerais para extrair a contração do tensor.
© 2019 Science X Network