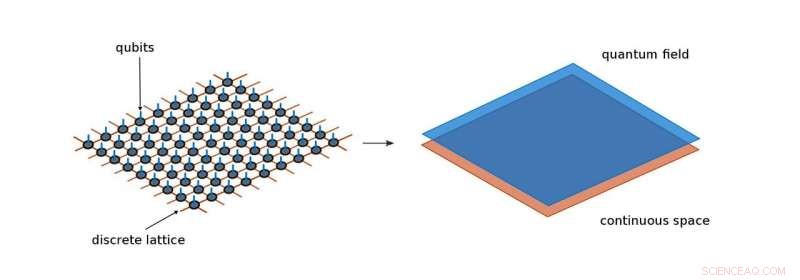
Os estados da rede tensorial padrão descrevem sistemas quânticos que vivem em um espaço discreto, ou treliça, por exemplo, uma matriz de qubits. Redes de tensores contínuos, por outro lado, encolher as distâncias da rede até que sejam infinitamente pequenas e, assim, restaurar a continuidade do espaço. Por aqui, eles podem lidar com campos quânticos mais diretamente. Crédito:Max Planck Institute of Quantum Optics
Calcular a dinâmica de muitas partículas quânticas em interação com precisão é uma tarefa assustadora. No entanto, existe um método de cálculo promissor para tais sistemas:redes de tensores, que estão sendo pesquisados na divisão de teoria do Instituto Max Planck de Óptica Quântica. O foco inicial da rede de tensores estava em partículas quânticas restritas a uma rede, assim como ocorrem em cristais, por exemplo, ou nos registros quânticos de futuros computadores quânticos. Em um novo jornal, o pesquisador de pós-doutorado Antoine Tilloy e o diretor da divisão de teoria Ignacio Cirac conseguiram estender essa abordagem ao continuum. Uma meta a longo prazo é um método de cálculo elegante para as teorias quânticas de campo que descreva as forças básicas da física.
Descrever os sistemas nos quais muitas partículas quânticas interagem e produzem coletivamente novos fenômenos é um dos desafios fundamentais da física. Um exemplo desse fenômeno quântico de muitos corpos é a supercondutividade. A dificuldade em questão é que as partículas influenciam umas às outras. Como resultado, as equações da mecânica quântica que descrevem este comportamento coletivo podem ser derivadas, mas não resolvido exatamente.
Na mecânica quântica, a equação dinâmica deve capturar todos os estados possíveis em que o sistema potencialmente pode estar. E pode haver muitos. Um exemplo atualmente popular na física são os bits quânticos. Eles são obtidos, por exemplo, de elétrons especialmente preparados ou átomos eletricamente carregados. Esses qubits têm dois estados opostos, que pode assumir os valores zero e um. Mas, ao contrário de um bit "clássico", o qubit também pode estar localizado em qualquer superposição desses dois estados. Se alguém agora acopla dois qubits com uma chamada porta quântica, o espaço matemático abstrato de todos os estados quânticos possíveis dobra. E cada qubit adicional o duplica novamente. Processadores e memórias de dados de computadores convencionais são literalmente invadidos por esse número exponencialmente crescente de possíveis estados quânticos. Mesmo os supercomputadores falham depois de mais do que algumas dezenas de qubits. Apenas computadores quânticos, obedecendo às próprias regras da mecânica quântica, um dia será capaz de lidar com a dinâmica de sistemas quânticos maiores.
Tornando o incalculável calculável
O exemplo dos qubits se encaixa, porque Ignacio Cirac e seus colegas estão entre os pioneiros neste campo emergente da tecnologia da informação quântica. O método de "redes de tensores, "que é o assunto deste artigo, também se origina neste campo de pesquisa. Ele permite reduzir inteligentemente o espaço gigantesco de todos os estados quânticos possíveis de um sistema multipartículas a um tamanho calculável. "Imagine todos os estados quânticos possíveis de um sistema de muitas partículas como uma grande área circular, "explica Antoine Tilloy." Mas os estados que são realmente relevantes para o nosso sistema cabem dentro de um círculo muito menor. "A arte agora é encontrar este pequeno círculo em um espaço matemático abstrato, e é isso que as redes tensor podem fazer.
Tilloy é pesquisador de pós-doutorado no grupo de Cirac e juntos acabam de publicar um artigo sobre redes tensoriais na revista. Revisão Física X . Originalmente, os físicos os aplicaram a matrizes de qubits individuais. As redes de tensores estavam, portanto, inicialmente contando com uma grade de objetos matemáticos abstratos - um pouco como um colar de pérolas matemáticas, vivendo em posições discretas.
As redes de tensores provaram ser uma ferramenta de sucesso para transportar cálculos para uma grande classe de sistema quântico confinado a grades. Esse sucesso deu a grupos de pesquisa teórica em todo o mundo uma ideia:este método também poderia ser aplicado a sistemas físicos que não vivem em grades, mas sim no espaço contínuo? Resumidamente, a resposta é sim. Na verdade, o método de redes tensoriais pode ser estendido ao continuum e é isso que Tilloy e Cirac demonstraram em seu novo trabalho.
Nova ferramenta para teorias quânticas de campo
As chamadas teorias quânticas de campo podem ser um importante campo de aplicação para esta nova caixa de ferramentas. Essas teorias constituem a base da cosmovisão física atual. Eles descrevem com precisão como três das quatro forças básicas da física funcionam de acordo com a mecânica quântica. Essas forças são mediadas por partículas virtuais que existem apenas durante o curto período de tempo necessário para transmitir sua força.
Na força elétrica, por exemplo, as partículas mediadoras são quanta virtuais de luz. "Isso se enquadra no que é conhecido como eletrodinâmica quântica e é bem compreendido, "diz Tilloy." As coisas ficam mais complicadas com o que é conhecido como cromodinâmica quântica. "QCD, como é chamado brevemente, descreve as forças entre os quarks, que por sua vez formam os blocos de construção dos núcleos atômicos, os prótons e nêutrons. Gluons, "partículas adesivas, "medeiam a força mais forte da física. E isso" cola "os quarks.
Mas, ao contrário dos fótons virtuais, os glúons também podem influenciar fortemente uns aos outros. Essa "auto-interação" leva ao fato desagradável de que as equações da QCD só podem ser resolvidas em casos limítrofes, com energia muito alta. Para energias mais baixas - o estado normal da matéria em nosso ambiente - isso não é possível. Por esta razão, os físicos até agora têm que trabalhar com soluções aproximadas. O passo padrão aqui é quebrar o continuum em uma grade artificial de pontos para os quais um computador poderoso pode calcular soluções aproximadas.
"Esta etapa de discretização é complexa, "diz Tilloy. Além disso, tais simplificações sempre têm a desvantagem de quebrar uma simetria fundamental da natureza ao dividir o contínuo em uma grade de pontos discretos. Eles são, portanto, forçados a se afastar da física real. O método de redes de tensores contínuos pode fornecer ajuda aqui, porque não requer essa discretização prévia do espaço. Talvez o comportamento de quarks e glúons em baixas energias um dia seja compreendido. Hoje ainda é um problema aberto, mas as redes de tensores contínuos recentemente descobertas podem já fazer parte da solução.