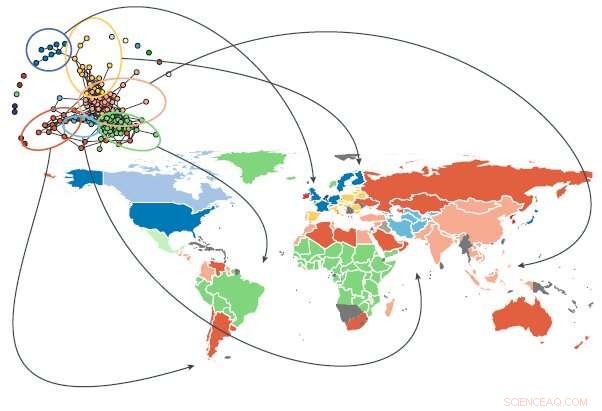
Crédito:Instituto de Física de Leiden
Os cientistas muitas vezes precisam entender os sistemas complexos sem conhecer os parâmetros importantes ou mesmo sem acesso a todas as informações. Uma colaboração de teóricos de rede relatou um quadro comum para abordar esses problemas usando apenas uma ferramenta.
Os economistas tentam prever crises financeiras e os físicos querem entender os sistemas que contêm muitas partículas. Contudo, ambos os problemas são notoriamente desafiadores. Muitas vezes, os pesquisadores precisam entender um sistema sem informações completas. E mesmo que tenham todas as informações, sistemas complexos ainda são difíceis de entender por causa das muitas ligações entre os componentes. Uma ampla gama de disciplinas científicas enfrenta essas questões.
Cientistas da área de pesquisa da teoria de redes estão trabalhando em ferramentas para problemas como reconstrução de redes e detecção de padrões. Contudo, a maioria dessas ferramentas funciona em apenas um problema. Agora, uma colaboração de teóricos de redes da Escola de Estudos Avançados IMT em Lucca (Itália), A Universidade de Leiden e o Conselho Italiano de Pesquisa (CNR) publicaram um artigo de revisão na edição inaugural da nova revista Nature Reviews Physics que fornece um quadro comum para resolver vários problemas com uma ferramenta.
Reconstrução de rede
Junto com seus co-autores, Diego Garlaschelli (IMT Lucca / Leiden) desenvolveu métodos para reconstruir redes sem acesso a todas as informações. Isso é relevante, por exemplo, no mundo financeiro, onde os bancos são apenas obrigados a divulgar seu débito e crédito total. Eles não fornecem informações sobre a quem eles emprestam ou tomam emprestado.
Essa falta de conhecimento muitas vezes implica um "risco oculto". Se o banco A emprestou dinheiro ao banco B, que, por sua vez, emprestou dinheiro a um banco C instável, então o banco A se torna instável, também. Quando os bancos centrais testaram várias ferramentas para reconstruir um sistema bancário, o proposto por Garlaschelli e coautores acabou por ser o de maior sucesso. Outros testes independentes forneceram o mesmo resultado.
Detecção de padrão
A equipe também trabalha na detecção de padrões. Nesse caso, os pesquisadores têm informações completas sobre um sistema complexo e tentam encontrar uma estrutura. Eles enfrentam dois problemas principais:Não se sabe quais são as propriedades importantes, e existem muitos parâmetros. O primeiro problema é resolvido criando um sistema aleatório que retém algumas características do mundo real e comparando-as com a vida real.
Garlaschelli diz, "Nós criamos, por exemplo, um sistema financeiro com links aleatórios entre bancos sob a condição de que cada banco retenha o mesmo número de links que tem no mundo real, e compará-lo ao sistema bancário holandês. A partir desta comparação, identificamos as propriedades importantes do sistema e até encontramos sinais de alerta antecipado para a crise de 2008. "O segundo problema é resolvido deduzindo analiticamente equações para as probabilidades de pares de nós serem conectados. Isso elimina a necessidade de processar numericamente uma grande quantidade de parâmetros .
Quadro comum
O artigo de revisão em Nature Reviews Physics fornece um quadro comum em que uma ferramenta pode ser aplicada tanto à reconstrução da rede quanto à detecção de padrões, e até mesmo a aspectos fundamentais da física estatística. Garlaschelli diz, "Nós temos, por exemplo, descobri que, em alguns casos, redes se comportam como um intermediário entre os sistemas Fermi-Dirac, onde as partículas não podem estar no mesmo estado, e sistemas Bose-Einstein, onde essa restrição não existe. Mais recentemente, identificamos um novo mecanismo responsável pela quebra de uma suposição centenária na física estatística - a saber, a equivalência de conjuntos canônicos e microcanônicos, que são tradicionalmente usados para descrever sistemas sob restrições suaves e rígidas, respectivamente. "