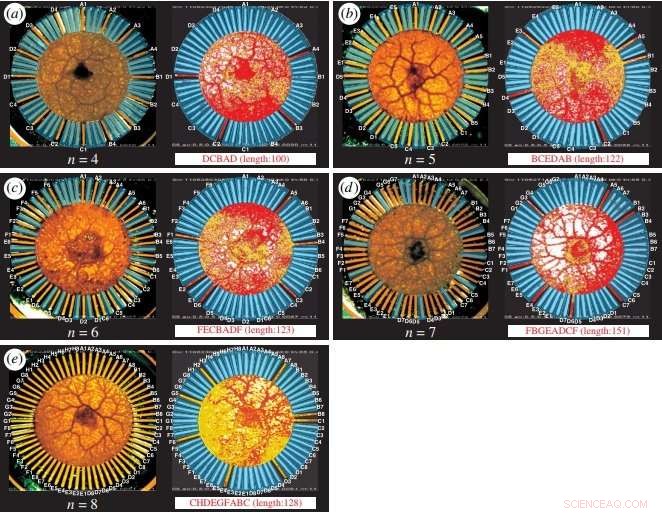
Soluções de TSP obtidas pelo sistema de computação baseado em ameba para 4, 5, 6, 7, e 8 cidades. Crédito:Zhu et al. © 2018 Royal Society Open Science
Os pesquisadores demonstraram que uma ameba - um organismo unicelular consistindo principalmente de protoplasma gelatinoso - tem habilidades de computação únicas que podem um dia oferecer uma alternativa competitiva aos métodos usados por computadores convencionais.
Os pesquisadores, liderado por Masashi Aono na Universidade Keio, designou uma ameba para resolver o Problema do Caixeiro Viajante (TSP). O TSP é um problema de otimização em que o objetivo é encontrar o caminho mais curto entre várias cidades, para que cada cidade seja visitada exatamente uma vez, e os pontos inicial e final são iguais.
O problema é NP-difícil, o que significa que conforme o número de cidades aumenta, o tempo necessário para um computador resolvê-lo cresce exponencialmente. A complexidade se deve ao grande número de soluções possíveis. Por exemplo, para quatro cidades, existem apenas três rotas possíveis. Mas para oito cidades, o número de rotas possíveis aumenta para 2520.
No novo estudo, os pesquisadores descobriram que uma ameba pode encontrar soluções razoáveis (quase ideais) para o TSP em um período de tempo que cresce apenas linearmente à medida que o número de cidades aumenta de quatro para oito. Embora os computadores convencionais também possam encontrar soluções aproximadas no tempo linear, a abordagem da ameba é completamente diferente dos algoritmos tradicionais. Como os cientistas explicam, a ameba explora o espaço da solução redistribuindo continuamente o gel em seu corpo amorfo a uma taxa constante, bem como processando feedback óptico em paralelo em vez de serialmente.
Embora um computador convencional ainda consiga resolver o TSP muito mais rápido do que uma ameba, especialmente para tamanhos pequenos de problemas, os novos resultados são intrigantes e podem levar ao desenvolvimento de novos computadores analógicos que derivam soluções aproximadas de problemas computacionalmente complexos de tamanhos muito maiores no tempo linear.
Como funciona
O tipo específico de ameba que os cientistas usaram foi um plasmódio ou "verdadeiro bolor limoso, "que pesa cerca de 12 mg e consome flocos de aveia. Essa ameba deforma continuamente seu corpo amorfo ao fornecer e retirar repetidamente o gel a uma velocidade de cerca de 1 mm / segundo para criar apêndices semelhantes a pseudópodes.
Em seus experimentos, os pesquisadores colocaram a ameba no centro de um chip estrelado, que é uma placa redonda com 64 canais estreitos projetando-se para fora, e, em seguida, coloque o chip no topo de uma placa de ágar. A ameba está confinada dentro do chip, mas ainda pode mover para os 64 canais.
A fim de maximizar sua absorção de nutrientes, a ameba tenta se expandir dentro do chip para entrar em contato com o máximo de ágar possível. Contudo, a ameba não gosta de luz. Uma vez que cada canal pode ser iluminado seletivamente pela luz, é possível forçar a ameba a recuar dos canais iluminados.
Para modelar o TSP, cada canal no chip estrelado representa uma cidade ordenada na rota do vendedor. Por exemplo, no caso de quatro cidades rotuladas de A-D, se a ameba ocupa os canais A4, B2, C1, e D3, então a solução correspondente para o TSP é C, B, D, UMA, C.
A fim de guiar a ameba em direção a uma solução ótima ou quase ótima, a chave está em controlar a luz. Para fazer isso, os pesquisadores usam um modelo de rede neural em que a cada seis segundos o sistema atualiza quais canais são iluminados. O modelo incorpora informações sobre a distância entre cada par de cidades, bem como feedback da posição atual da ameba nos canais.
O modelo garante que a ameba encontre uma solução válida para o TSP de algumas maneiras. Por exemplo, uma vez que a ameba ocupou uma certa fração de um canal particular, diga A3, em seguida, canais A1, A2, e todos os outros canais "A" são iluminados para impedir que a cidade A seja visitada duas vezes. Também, B3, C3, D3, e todos os outros canais "3" são iluminados para proibir visitas simultâneas a várias cidades.
O modelo considera as distâncias entre as cidades, tornando mais fácil iluminar canais que representam cidades com distâncias mais longas do que com distâncias mais curtas. Por exemplo, digamos que a ameba ocupa o canal B2, e começou a invadir os canais C3 e D3 em quantidades iguais, e a distância entre as cidades B e C é 100, enquanto a distância entre as cidades B e D é 50. A maior distância entre B e C eventualmente faz com que o sistema ilumine o canal C3, fazendo com que a ameba recue desse canal, mas permitindo que ela continue se movendo para D3.
Geral, modelar o TSP com uma ameba atrai a tendência natural da ameba de buscar um equilíbrio estável. Como canais que representam rotas mais curtas têm menos probabilidade de serem iluminados, a ameba pode se espalhar nesses canais e continuar a explorar outros canais não iluminados para maximizar sua área de superfície na placa de ágar.
Os pesquisadores também desenvolveram uma simulação de computador chamada AmoebaTSP que imita algumas das principais características de como a ameba trata o problema, incluindo o movimento contínuo do gel à medida que é fornecido a uma taxa constante e retirado de vários canais.
"Em nosso chip estrelado para resolver o n -city TSP, a área total do corpo da ameba torna-se n quando a ameba finalmente encontra uma solução aproximada, "Aono disse Phys.org . "Parece haver uma 'lei' de que a ameba fornece seu recurso gelatinoso para se expandir nos canais não iluminados a uma taxa constante, dizer, x . Essa lei seria mantida mesmo quando alguns recursos voltassem dos canais iluminados. Então, o tempo necessário para expandir a área do corpo n representar a solução torna-se n / x . Este mecanismo seria a origem do tempo linear, e foi reproduzido por nosso modelo de simulação de computador.
"Mas ainda, o mecanismo pelo qual a ameba mantém a qualidade da solução aproximada, isso é, o comprimento da rota curta, permanece um mistério. Parece que os movimentos espacial e temporalmente correlacionados das partes ramificadas da ameba localizadas em canais distantes são a chave. Cada um desses ramos está oscilando seu volume com alguma "memória" temporal em experiências iluminadas. Grupos de filiais realizam sincronização e dessincronização para compartilhar informações, embora estejam espacialmente distantes. "
No futuro, os pesquisadores planejam melhorar ainda mais as habilidades de computação da ameba.
"Investigaremos mais detalhadamente como essas dinâmicas oscilatórias espaço-temporais complexas aumentam o desempenho computacional na busca de soluções de alta qualidade em menos tempo, "disse o co-autor Song-Ju Kim da Universidade Keio." Se pudesse ser esclarecido, o conhecimento contribuirá para a criação de novos computadores analógicos que explorem a dinâmica espaço-temporal da corrente elétrica em seu circuito.
"Claro, executando alguns outros algoritmos em computadores digitais tradicionais para o tempo linear, podemos derivar soluções aproximadas para o TSP. Por outro lado, ao executar nossos modelos de simulação (AmoebaTSP ou suas versões desenvolvidas) nos computadores tradicionais como fizemos neste estudo, a dinâmica espaço-temporal analógica e paralela requer tempo não linear para simulá-los como processos digitais e seriais. Portanto, estamos tentando obter soluções de qualidade muito superior às derivadas das tradicionais, executando nossos modelos nos computadores analógicos por tempo linear ou menor. "
Os pesquisadores também esperam que, fabricando um chip maior, a ameba será capaz de resolver problemas de TSP com centenas de cidades, embora isso requeira dezenas de milhares de canais.
© 2018 Science X Network