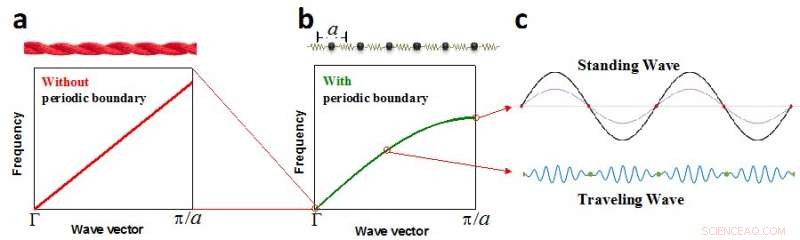
(a) dispersão linear de fônons com base na suposição de onda elástica-acústica, (b) dispersão de seno de fônon considerando a condição de contorno periódica, (c) onda estacionária em rede (topo) e onda progressiva (parte inferior). Crédito:Science China Press
A condutividade térmica da rede afeta fortemente as aplicações de materiais relacionados à funcionalidade térmica, como gerenciamento térmico, revestimentos de barreira térmica e termoelétricas. Para entender a condutividade térmica da rede de maneira mais quantitativa e econômica, muitos pesquisadores têm dedicado seus esforços e desenvolvido alguns modelos físicos usando dispersões de fônons aproximadas ao longo do século passado.
A maioria desses modelos usa uma dispersão linear de fônons, proposto por Debye em 1912 com base em uma suposição de onda elástica-acústica (Fig. 1a), enquanto outros modelos envolvem parâmetros de ajuste na dispersão de fônons ou carecem de equações detalhadas para propriedades de transporte de fônons. A dispersão linear de fônons de Debye oferece muitas simplificações nas propriedades de transporte de fônons, e foi a aproximação mais comum no século passado. A dispersão linear de Debye prevê com sucesso a dependência T3 da capacidade de calor em temperaturas muito baixas, e a capacidade de calor se aproxima do limite de Dulong-Petit em altas temperaturas. Contudo, a natureza da periodicidade em arranjos atômicos leva a uma condição de contorno periódica para vibrações de rede em sólidos (Fig. 1b), que na verdade cria ondas estacionárias de rede nos limites de Brillouin (Fig. 1c). Isso não satisfaz a suposição de onda elástica acústica de Debye, como proposto por Born e von Karman (BvK) em 1912 - o mesmo ano em que Debye propôs a dispersão linear.
Isso resulta em um desvio significativo da dispersão de Debye para materiais cristalinos periódicos quando os fônons com vetores de onda estão próximos dos limites de Brillouin (fônons de alta frequência). Quando esses fônons estão envolvidos no transporte de fônons (ou seja, em temperaturas não extremamente baixas), A dispersão de Debye leva a uma superestimação da condutividade térmica da rede devido à superestimação da velocidade do grupo para esses fônons de alta frequência, conforme observado em materiais com centenas de condutividade térmica de rede medida conhecida e detalhes necessários para uma previsão de modelo de tempo e custo-benefício para o nosso melhor conhecimento (Fig. 2g e h mostrando um desvio absoluto médio de ~ + 40%). Além disso, A dispersão de Debye superestima o limite inferior teoricamente disponível da condutividade térmica da rede também, levando as violações da condutividade térmica da rede medida a ser ainda menor do que o mínimo teórico atual previsto (com base no modelo Debye-Cahill), conforme observado em dezenas de materiais.
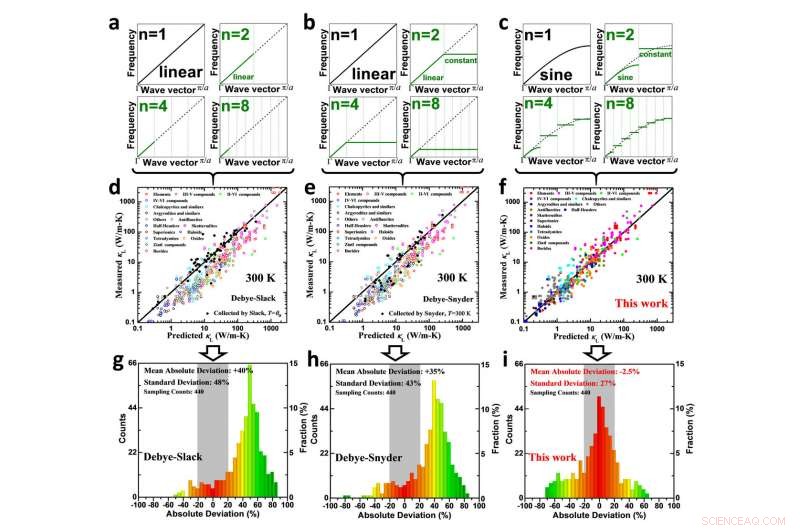
Comparação na dispersão de fônons (a, bec), medido a condutividade térmica da rede versus previsão (d, e e f) e as análises de erro correspondentes (g, hei) para o modelo Debye-Slack (a, d e g), Modelo Debye-Snyder (b, e e h) e aquele desenvolvido neste trabalho considerando a condição de contorno periódica (c, g e i) para sólidos cristalinos. Crédito:Science China Press
Este trabalho leva em consideração a condição de contorno BvK, e revela que o produto das dispersões acústicas e ópticas produz uma função seno. No caso em que a massa (ou a constante de força) o contraste entre os átomos é grande, a dispersão acústica tende a ser uma função seno. Este tipo de dispersão senoidal existe de fato tanto nos materiais mais simples quanto nos mais complexos. Aproximando a dispersão acústica para ser seno, a condição de contorno BvK subsequentemente reduz os ramos ópticos restantes a uma série de modos localizados com uma série de frequências constantes. Enquanto os cálculos de primeiros princípios permitem uma dispersão de fônons mais detalhada, um desenvolvimento de dispersão de fônons racionalizada para uma previsão de transporte de fônons com custo reduzido e em tempo é significativo devido ao consumo de tempo e alto custo computacional para cálculos de primeiros princípios.
Este trabalho utiliza a racionalização acima mencionada de dispersões de fônons, o que permite que ambas as contribuições para a condutividade térmica da rede de fônons acústicos e ópticos sejam incluídas. Esta melhoria nas dispersões de fônons melhora significativamente a precisão de uma previsão de tempo e custo-benefício na condutividade térmica da rede de sólidos sem quaisquer parâmetros de ajuste (Fig. 2c, mostrando um desvio absoluto médio de apenas -2,5%), e, portanto, oferece um design mais preciso de sólidos com condutividade térmica de rede esperada. Além disso, este trabalho remove com sucesso a contradição da condutividade térmica da rede medida sendo ainda menor do que o mínimo teórico previsto com base em uma dispersão linear de Debye (Fig. 3). Isso forneceria a possibilidade teórica de racionalizar a condutividade térmica da rede para ser menor do que se pensa atualmente, abrindo mais oportunidades para o avanço de materiais termicamente resistivos para aplicações, incluindo termelétricas.
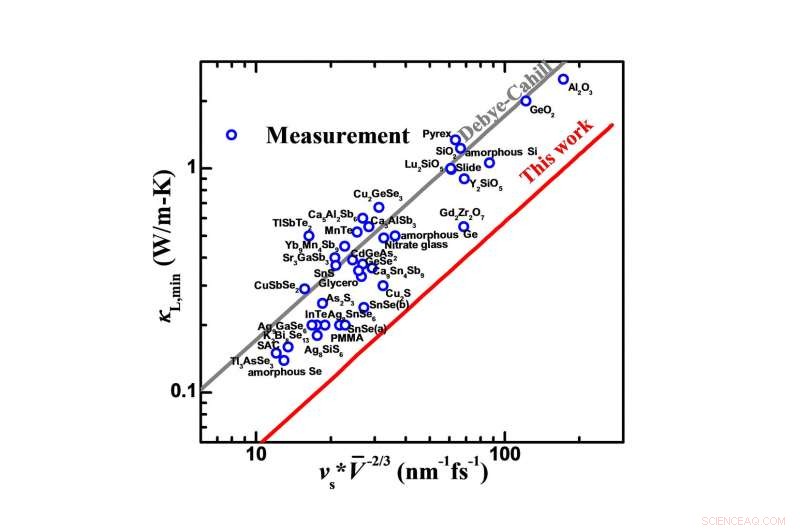
Comparação na condutividade térmica mínima medida da rede (? L, min) e previsões baseadas em uma dispersão desenvolvida de acordo com a condição de contorno periódica ou em uma dispersão linear de Debye (modelo Debye-Cahill). Crédito:Science China Press