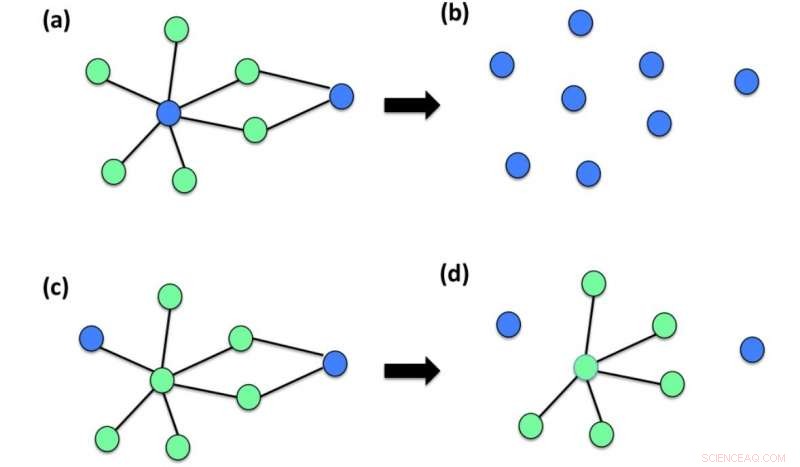
Diferentes realizações do dano inicial são aqui mostradas como mais ou menos prejudiciais para uma rede. O painel (a) mostra um dano inicial de uma rede conectada afetando exclusivamente dois dos N =8 nós da rede (nós azuis sindicados danificados nós verdes indicam nós não danificados). O painel (b) mostra que esse dano inicial é muito prejudicial para a rede e resulta em um componente gigante de tamanho R =1. O painel (c) mostra outra configuração de dano inicial da mesma rede que afeta apenas dois nós da rede. Neste caso, o painel (d) mostra que o efeito dos danos é reduzido e a maior parte da rede permanece conectada resultando em um componente gigante R =6. Crédito:Ginestra Bianconi
Uma estrutura teórica que explica o risco de eventos raros que causam grandes interrupções em redes complexas, como um apagão em uma rede elétrica, foi proposto por um matemático da Queen Mary University of London.
Eventos raros podem desmontar abruptamente uma rede com consequências muito mais graves do que o normal e entender sua probabilidade é essencial para reduzir as chances de que ocorram.
Uma rede é formada por um conjunto de nós e os links entre eles. Por exemplo, as redes de energia são redes cujos nós são estações de energia conectadas pela rede elétrica. Da mesma forma, uma rede ecológica, ao qual a estrutura pode ser aplicada, é formado por espécies conectadas por interações ecológicas como uma relação predador-presa.
Normalmente, se alguns dos nós estiverem danificados, redes como essas são robustas o suficiente para permanecerem funcionais, mas em raras ocasiões, danos específicos podem levar ao desmantelamento de toda a rede e causar grandes apagões ou mudanças de regime ecológico, como um colapso ecológico.
Os matemáticos costumam usar a teoria da percolação, um ramo bem desenvolvido da matemática aplicada que estuda a resposta de uma rede ao dano de uma fração aleatória de seus nós, para lançar luz sobre esses fenômenos. Contudo, esta teoria é capaz apenas de caracterizar a resposta média de uma rede a danos aleatórios. Portanto, a previsão do comportamento médio não pode ser usada para estimar o risco de colapso da rede como resultado de um evento raro.
Este estudo estabelece uma teoria de grande desvio de percolação que caracteriza a resposta de uma rede a eventos raros. O referencial teórico proposto capta corretamente o efeito de configurações raras de danos que podem ser observadas em redes reais. Curiosamente, o trabalho revela que as transições de percolação descontínua - colapsos abruptos de uma rede - estão ocorrendo assim que eventos raros são levados em consideração.
A estrutura teórica pode permitir o desenvolvimento de estratégias para sustentar as redes, identificando quais nós precisam ser preservados para evitar um colapso.
Ginestra Bianconi, autor do estudo, disse:"Há uma necessidade urgente de avaliar o risco de colapso em resposta a configurações raras de danos iniciais. Este resultado lança luz sobre a fragilidade oculta das redes e seu risco de colapso repentino e pode ser especialmente útil para compreender os mecanismos para evitar o desmantelamento catastrófico de redes reais. "
Ela acrescentou:"É importante estimar o risco de uma cascata dramática de falhas porque você deseja reduzir o risco. No projeto de uma rede elétrica que deve fornecer energia a um país inteiro, você deseja evitar eventos raros nos quais você tem grandes apagões, ou no desenho de estratégias de preservação de um ecossistema que atualmente é diversificado e próspero você deseja saber qual é a probabilidade de um colapso ecológico repentino e extinção em massa. Portanto, é necessário entender esse risco de esses eventos acontecerem. "
O presente estudo de grandes desvios de percolação considera exclusivamente a percolação de nós em redes únicas como as mencionadas. Contudo, Ginestra Bianconi sugere que a metodologia delineada pode ser estendida ao estudo de modelos mais detalhados de propagação de falhas de eventos.