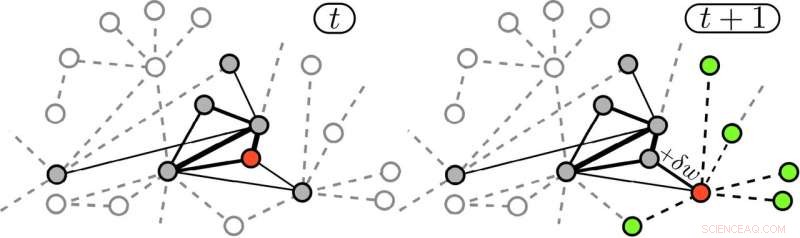
Caminhadas aleatórias reforçadas por bordas produzem uma coevolução da rede com a dinâmica dos caminhantes. No momento t, o caminhante está no nó vermelho e já visitou os nós cinza, enquanto os nós sombreados ainda estão inexplorados. As larguras das arestas são proporcionais aos seus pesos. No momento t + 1, o caminhante mudou-se para um nó vizinho (vermelho), e o peso da aresta usada foi reforçado por δw. Neste ponto, o caminhante irá preferencialmente voltar, embora também possa acessar o conjunto de 'possíveis adjacentes' (verde). Crédito:Iacopo Iacopini
Pesquisadores da Queen Mary University of London desenvolveram um modelo matemático para o surgimento de inovações.
Estudar processos criativos e compreender como surgem as inovações e como as novidades podem desencadear novas descobertas pode levar a intervenções eficazes para alimentar o sucesso e o crescimento sustentável da sociedade.
Os resultados empíricos mostraram que a forma como as novidades são descobertas segue padrões semelhantes em uma variedade de contextos diferentes, incluindo a ciência, artes, e Tecnologia.
O estudo, publicado em Cartas de revisão física , introduz uma nova estrutura matemática que reproduz corretamente a taxa em que as novidades surgem em sistemas reais, conhecido como lei de Heaps, e pode explicar por que as descobertas são fortemente correlacionadas e geralmente vêm em grupos.
Ele faz isso traduzindo a teoria do 'possível adjacente', inicialmente formulado por Stuart Kauffman no contexto de sistemas biológicos, na linguagem de redes complexas. O possível adjacente é o conjunto de todas as novas oportunidades que se abrem quando uma nova descoberta é feita. As redes surgiram como uma forma poderosa de investigar sistemas do mundo real, capturando as relações essenciais entre os componentes, e modelar a estrutura oculta por trás de muitos fenômenos sociais complexos.
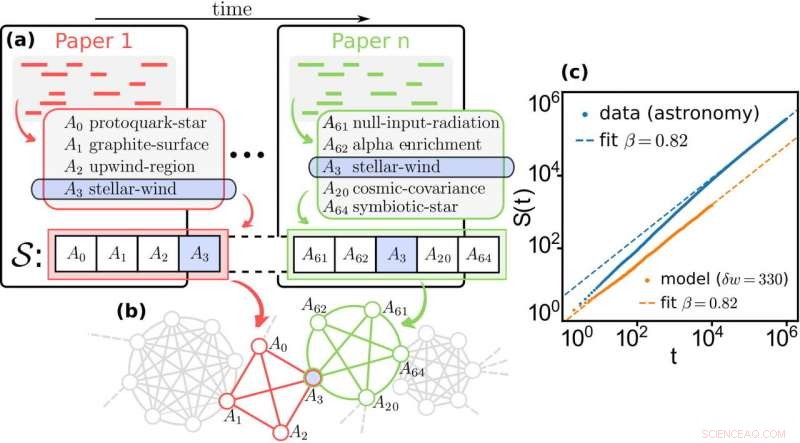
Crescimento do conhecimento em ciências. (a) Uma sequência empírica de conceitos científicos S é extraída de uma sequência temporalmente ordenada de artigos por concatenação, para cada campo científico, os conceitos relevantes presentes nos resumos. (b) A rede de relações entre os conceitos é construída ligando todos os conceitos que aparecem no mesmo resumo. A rede é então usada como uma estrutura subjacente para executar nosso modelo de passeio aleatório reforçado por borda. (c) O modelo é então ajustado aos dados empíricos selecionando a quantidade de reforço δw que reproduz o expoente de Heaps β obtido pelo ajuste da curva de Heaps extraída de S como uma lei de potência. Crédito:Iacopo Iacopini
Nesse trabalho, as redes são usadas para modelar o espaço subjacente de relações entre conceitos.
Professor Vito Latora, autor principal, da Queen Mary's School of Mathematical Sciences, disse:"Esta pesquisa abre novas direções para a modelagem de inovação, junto com uma nova estrutura que pode se tornar importante na investigação de tecnologia, biológico, artístico, e sistemas comerciais. "
Ele acrescentou:"Estudar os processos através dos quais surgem as inovações pode ajudar a compreender os principais ingredientes por trás de uma ideia vencedora, uma tecnologia inovadora ou uma atividade comercial de sucesso, e é fundamental para conceber decisões eficazes com base em dados, estratégias, e intervenções para fomentar o sucesso e o crescimento sustentável da nossa sociedade. "
No estudo, o processo de descoberta é modelado como uma classe particular de passeios aleatórios, chamadas caminhadas 'reforçadas', em uma rede subjacente de relações entre conceitos e ideias. Uma inovação corresponde à primeira visita a um site da rede, e cada vez que um caminhante muda de um conceito para outro, essa associação (uma borda na rede) é reforçada para que seja usada com mais frequência no futuro. Os pesquisadores chamaram isso de modelo de 'passeio aleatório reforçado por bordas'.
Para mostrar como o modelo funciona em um caso real, eles também construíram um conjunto de dados de 20 anos de publicações científicas em diferentes disciplinas, como astronomia, ecologia, economia e matemática para analisar o surgimento de novos conceitos. Isso mostrou que, apesar de sua simplicidade, o modelo de passeio aleatório reforçado por bordas é capaz de reproduzir como o conhecimento cresce na ciência moderna.
O professor Vito Latora acrescentou:"O quadro que apresentamos constitui uma nova abordagem para o estudo dos processos de descoberta, em particular aqueles para os quais a rede subjacente pode ser reconstruída diretamente a partir de dados empíricos, por exemplo, usuários que ouvem música em uma rede de semelhança entre as músicas. Já estamos trabalhando nessa ideia, junto com uma versão estendida do nosso modelo, onde estudamos a exploração coletiva desses espaços em rede, considerando vários caminhantes ao mesmo tempo. "