A tangente é uma das três funções trigonométricas básicas, as outras duas sendo seno e cosseno. Essas funções são essenciais para o estudo de triângulos e relacionam os ângulos do triângulo aos seus lados. A definição mais simples da tangente usa as proporções dos lados de um triângulo retângulo, e os métodos modernos expressam essa função como a soma de uma série infinita. As tangentes podem ser calculadas diretamente quando os comprimentos dos lados do triângulo retângulo são conhecidos e também podem ser derivados de outras funções trigonométricas.

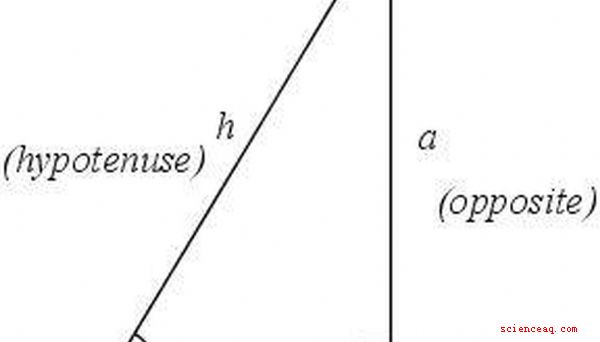
Identifique e rotule as partes de um triângulo retângulo. O ângulo reto estará no vértice C, e o lado oposto será a hipotenusa h. O ângulo &# x3B8; estará no vértice A e o vértice restante será B. O lado adjacente ao ângulo &# x3B8; será o lado be o lado oposto do ângulo &# x3B8; estará do lado a. Os dois lados de um triângulo que não são a hipotenusa são conhecidos como pernas do triângulo.


Defina a tangente. A tangente de um ângulo é definida como a razão entre o comprimento do lado oposto ao ângulo e o comprimento do lado adjacente ao ângulo. No caso do triângulo na Etapa 1, tan &# x3B8; \u003d a /b.


Determine a tangente para um triângulo retângulo simples. Por exemplo, as pernas de um triângulo retângulo isósceles são iguais, então a /b \u003d tan &# x3B8; \u003d 1. Os ângulos também são iguais, então &# x3B8; \u003d 45 graus. Portanto, tan 45 graus \u003d 1.


Derive a tangente das outras funções trigonométricas. Desde seno &# x3B8; \u003d a /he co-seno &# x3B8; \u003d b /h, então seno &# x3B8; /cosseno &# x3B8; \u003d (a /h) /(b /h) \u003d a /b \u003d tan &# x3B8 ;. Portanto, tan &# x3B8; \u003d seno &# x3B8; /cosine &# x3B8 ;.


Calcule a tangente para qualquer ângulo e precisão desejada:


sin x \u003d x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... cosseno x \u003d 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! A soma de dois algarismos distintos é igual a: a) x2 + x2 + x2 + x2 + x \u003d 0 /4! - x ^ 6/6! + ...)