A história geralmente começa no começo e depois relaciona eventos de desenvolvimento ao presente para que você possa entender como chegou até onde você está. Com a matemática, neste caso expoentes, fará muito mais sentido começar com uma compreensão e um significado atuais de expoentes e trabalhar de trás para a partir de onde eles vieram. Em primeiro lugar, vamos nos certificar de que você entende o que é um expoente porque pode ser bastante complicado. Neste caso, vamos mantê-lo simples.
Onde estamos agora
Esta é a versão da escola secundária, então todos nós devemos entender isso. Um expoente reflete um número multiplicado por si mesmo, como 2 vezes 2 é igual a 4. Na forma exponencial que poderia ser escrita 2², chamada de dois ao quadrado. O 2 elevado é o expoente e o 2 é o número base. Se você quisesse escrever 2x2x2, poderia ser escrito como 2³ ou dois para a terceira potência. O mesmo vale para qualquer número base, 8² é 8x8 ou 64. Você obtém. Você poderia usar qualquer número como base e o número de vezes que você deseja multiplicá-lo por si só se tornaria o expoente.
Onde os expoentes vêm?
A própria palavra vem do latim, expo, significado de e ponere, significando lugar. Enquanto o expoente palavra veio a significar coisas diferentes, o primeiro uso moderno registrado de expoente em matemática foi em um livro chamado "Arithemetica Integra", escrito em 1544 pelo escritor inglês e matemático Michael Stifel. Mas ele estava trabalhando simplesmente com uma base de dois, então o expoente 3 significaria o número de 2s que você precisaria multiplicar para obter 8. Ele ficaria assim 2³ = 8. A maneira como Stifel diria é um pouco atrasada quando comparada à maneira como pensamos sobre isso hoje. Ele diria "3 é o 'estabelecimento' de 8." Hoje, referiríamos a equação simplesmente como 2 cubos. Lembre-se, ele estava trabalhando exclusivamente com uma base ou fator 2 e traduzindo do latim um pouco mais literalmente do que hoje.
Aparentes ocorrências anteriores
Embora não seja 100% certo, parece que idéia de quadratura ou cubismo vai todo o caminho de volta aos tempos da Babilônia. Babilônia fazia parte da Mesopotâmia na área que agora consideramos o Iraque. A primeira menção conhecida da Babilônia é encontrada em um tablet datado do século 23 aC. E eles ainda estavam se dando bem com o conceito de expoentes, embora seu sistema de numeração (sumério, agora uma língua morta) use símbolos para rebaixar fórmulas matemáticas. Estranhamente, eles não sabiam o que fazer com o número 0, de modo que foi delineado por um espaço entre os símbolos.
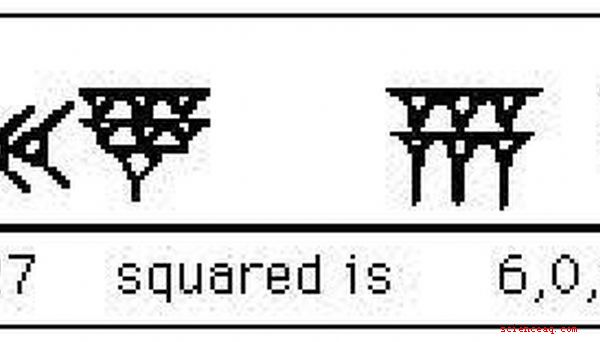
O que os primeiros expoentes pareciam
O sistema de numeração era obviamente diferente da matemática moderna. Sem entrar nos detalhes de como e por que foi diferente, basta dizer que eles escreveriam o quadrado de 147 como este. No sistema sexagesimal de matemática, que é o que os babilônios usavam, o número 147 seria escrito 2,27. Quadrando produziria em dias modernos, o número de número 21.609. Na Babilônia está escrito 6,0,9. Em sexagesimal 147 = 2,27 e quadratura dá o número 21609 = 6,0,9. Isto é o que a equação, como descobriu em outra tabuleta antiga, parecia. (Tente colocar isso na sua calculadora).
Por que expoentes?
E se, digamos, em uma fórmula matemática complexa, você precisar calcular algo realmente importante. Poderia ser qualquer coisa e é necessário saber o que 9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9 igualado. E havia muitos números tão grandes na equação. Não seria muito mais simples escrever 9³? Você pode descobrir o que esse número é se você se importa. Em outras palavras, é taquigrafia, assim como muitos outros símbolos em matemática são abreviados, denotando outros significados e permitindo que fórmulas complexas sejam escritas de maneira mais concisa e compreensível. Uma ressalva a ter em mente. Qualquer número elevado à potência zero é igual a 1. Essa é uma história para outro dia.