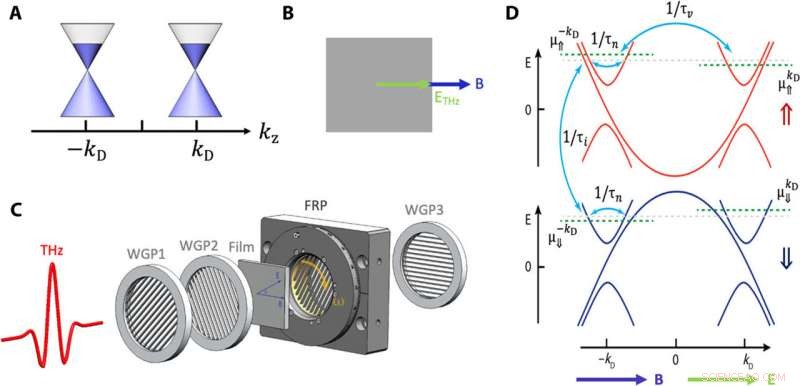
Dinâmica de carga da anomalia quiral em um DSM e a configuração experimental. (A) Ilustração esquemática da estrutura eletrônica de baixa energia do DSM Cd3As2. Ele hospeda dois nós Dirac 3D localizados ao longo do eixo kz. (B) A anomalia quiral é esperada quando o campo magnético CC e o campo elétrico THz são coalinhados. (C) Esquema do espectrômetro magnetoterahertz no domínio do tempo usado para coletar dados. O polarizador de grade de fio 1 (WGP1) e WGP2 são usados para produzir pulso terahertz polarizado linearmente com ETHz ∥ B ou ETHz ⊥ B. Um polarizador de rotação rápida (FRP) é usado para modular o campo elétrico terahertz por uma frequência próxima de 47 Hz. Com WGP3 e amplificador lock-in, a complexa matriz de transmissão pode ser determinada por meio de uma única medição com alta precisão. (D) Em um DSM com ETHz ∥ B, os estados 3D Dirac desenvolverão níveis Landau (LLs), que são dispersivos ao longo da direção do campo magnético. O zero LL fornece a corrente quiral. Uma série de taxas de relaxamento diferentes controlam a dinâmica de carga. 1 / τn é a taxa de espalhamento intranó (normal), 1 / τv é a taxa de espalhamento intervalado, e 1 / τi é a taxa de espalhamento entre os entrenós no mesmo vale de momento, mas para a outra variedade isospin. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
Os semimetais 3D Dirac e Weyl podem ser caracterizados por uma quiralidade de carga com o bloqueio paralelo ou antiparalelo do spin do elétron em seu momento. Esses materiais podem exibir um efeito magnético quiral associado à quase conservação da carga quiral. Nesse trabalho, Bing Cheng e uma equipe de pesquisa em física e astronomia da Universidade Johns Hopkins e ciência dos materiais na Universidade da Califórnia, Santa Barbara, usou espectroscopia magneto-terahertz para estudar o arsenieto de cádmio epitaxial (Cd 3 Como 2 ) filmes - um material amplamente explorado na física do estado sólido para extrair suas condutividades em função do efeito magnético quiral. Quando a equipe aplicou o campo, eles notaram uma resposta drástica marcadamente nítida - um modelo altamente aclamado de transporte eletrônico sugerido pelo físico Paul Drude há mais de 100 anos. A resposta Drude surgiu do contexto mais amplo deste sistema como uma assinatura definitiva de um novo canal de transporte consistente com a resposta quiral. A independência de campo da relaxação quiral estabeleceu que ela foi definida pela conservação aproximada do isospin na configuração.
A anomalia quiral
Algumas das demonstrações mais notáveis de estados topológicos da matéria surgem de sua resposta a campos eletromagnéticos. Por exemplo, Os isoladores topológicos são caracterizados por um efeito magnetoelétrico quantizado. Semimetais de Weyl e Semimetais de Dirac (WSM e DSM) são estados da matéria nos quais bandas de condução e valência tocam e se dispersam quase linearmente em torno de pares de nós no espaço de momento. Cada nó pode ser identificado por sua quiralidade em relação ao spin de uma partícula sem massa (com dispersão linear) orientada paralela ou antiparalela ao seu momento. Os sistemas Dirac são, portanto, semelhantes a duas cópias dos sistemas Weyl; em cada nó, existem dois conjuntos de bandas de distribuição linear com carga quiral oposta. Apesar de serem metais, Semimetais de Weyl e semimetais de Dirac mostraram efeitos de transporte distintos associados à quase conservação da carga quiral. A anomalia quiral, portanto, existia nos limites de transporte quântico e semiclássico. A carga quiral não é conservada em nenhum material real devido a violações da simetria quiral por meio de dispersões de bandas não lineares. Como resultado, a quase conservação da carga quiral é relativa à simetria quiral emergente de baixa energia. Embora o efeito existisse em regimes de transporte semiclássico e quântico, o efeito foi mais bem compreendido no limite quântico. A carga quiral não é precisamente conservada e é bombeada sob a ação de campos elétricos e magnéticos colineares, conhecidos como anomalia quiral. Os cientistas observaram uma magnetorresistência longitudinal negativa (NLMR) em vários sistemas semimetais de Dirac e semimetais de Weyl como consequência do efeito magnético quiral, embora o NLMR não seja causado exclusivamente por esse efeito.
Condutividade Terahertz em diferentes campos magnéticos. (A) ETHz ∥ B com B∥ (1¯10) para a amostra S1. A anomalia quiral leva a condutividade terahertz σ1 abaixo de 1 THz a ser aumentada gradualmente pelo campo magnético. (B) ETHz ⊥ B com B∥ (1¯10) para a amostra S1. A supressão da condutividade terahertz σ1 é a assinatura da magnetorresistência positiva, que geralmente é observado em campos magnéticos e elétricos perpendiculares. (C) ETHz ∥ B para B∥ (11¯¯¯¯2) amostra S2. (D) ETHz ⊥ B para B∥ (11¯¯¯¯¯2) amostra S2. (E e F) Comparações destes dados 0- e 7-T e suas diferenças para as amostras S1 e S2. Δσ1 é a condutividade quiral intrínseca da anomalia quiral. A área cinza destacada representa a força do efeito de bombeamento de carga, e sua largura define a taxa de relaxamento quiral. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914 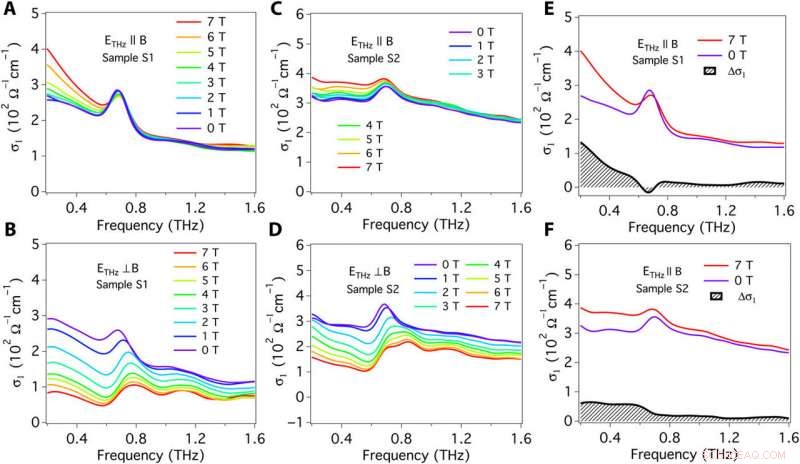
Um parâmetro chave que rege a anomalia quiral é a taxa de relaxamento quiral. As propriedades intrínsecas da anomalia quiral podem ser caracterizadas de forma mais convincente medindo diretamente a taxa de relaxamento quiral e as taxas de relaxamento intravalley. King et al. usaram espectroscopia magneto-terahertz para estudar os filmes finos epitaxiais de alta qualidade de semimetais de arseneto de cádmio de Dirac (Cd 3 Como 2 ) Este é um material ideal para investigações devido aos seus nódulos Dirac quádruplos degenerados que são protegidos por um C 4 simetria. Tipicamente, o Cd orientado de alta qualidade 3 Como 2 os filmes podem ser cultivados usando epitaxia de feixe molecular. Ao realizar experimentos de condutividade dependente de frequência, os cientistas extraíram a taxa de relaxamento quiral e as taxas de relaxamento intravalley diretamente. Eles então mediram dois Cd 3 Como 2 filmes e extraiu sua condutividade terahertz dependente do campo usando duas medições sem contato para evitar quaisquer artefatos associados com os caminhos de corrente não homogêneos que tendem a atormentar os experimentos de corrente contínua.
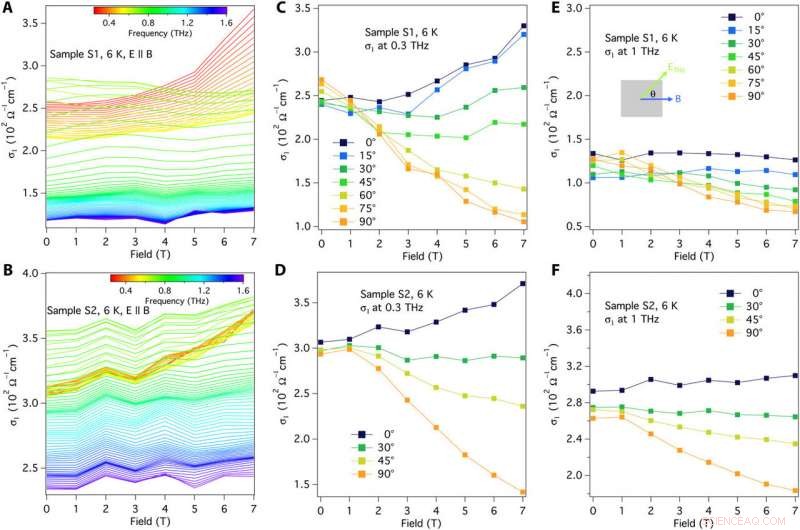
Condutividade Terahertz em diferentes campos magnéticos. Condutividade Terahertz σ1 em cada frequência (ver escala da barra de cores) em função do campo magnético de (A) amostra S1 e (B) amostra S2 com ETHz ∥ B. Condutividade Terahertz (em 0,3 THz) em função do campo magnético sob diferentes ângulos de polarização terahertz da amostra (C) S1 e (D) da amostra S2. A configuração do ângulo de polarização θ entre o campo elétrico terahertz e o campo magnético é mostrada pelo esquema em (E). Condutividade Terahertz (em 1 THz) como uma função do campo magnético sob diferentes ângulos de polarização terahertz da amostra (E) S1 e (F) amostra S2. Todos os dados foram obtidos a 6 K. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
Condutividade Terahertz e transporte quiral
Em seguida, a equipe investigou a condutividade terahertz em diferentes campos magnéticos e extraiu o bombeamento de carga dinâmica e o relaxamento da anomalia quiral usando ajustes Drude-Lorentz. Eles notaram um notável efeito induzido por campo, resultando em um aumento apenas da condutividade de baixa frequência. Contudo, isso não resultou de uma mudança na taxa de espalhamento normal ou mudança na densidade da portadora do material, mas contou com o aparecimento de um canal de transporte paralelo com uma nova escala de frequência. O efeito também não foi associado com espalhamento dependente de spin, que normalmente se manifestaria como uma mudança geral na taxa de espalhamento. O surgimento de um canal de transporte adicional e uma nova escala de tempo estavam precisamente de acordo com as expectativas teóricas para a anomalia quiral. O transporte quiral ocorreu por meio de um aumento do potencial eletroquímico efetivo por meio do equilíbrio entre o bombeamento quiral e o espalhamento dos internódios. Para distinguir uma corrente quiral em estado estacionário, a taxa de espalhamento quiral tinha que ser menor do que a taxa de relaxamento intravalley. Nos experimentos, Cheng et al. observou que a taxa de espalhamento quiral é de aproximadamente um quarto da taxa de relaxamento intravalley em ambas as amostras. Os cientistas compararam este tamanho relativo à luz da teoria prevalecente e esperam conduzir mais estudos nesta área no futuro. A equipe também interpretou os recentes experimentos de terahertz não lineares relativos ao relaxamento quiral que mostraram uma taxa lenta devido à maior separação de nós no arseneto de tântalo cristalino semimetal de Weyl (taAs) e / ou a falta de espalhamento de isospin.
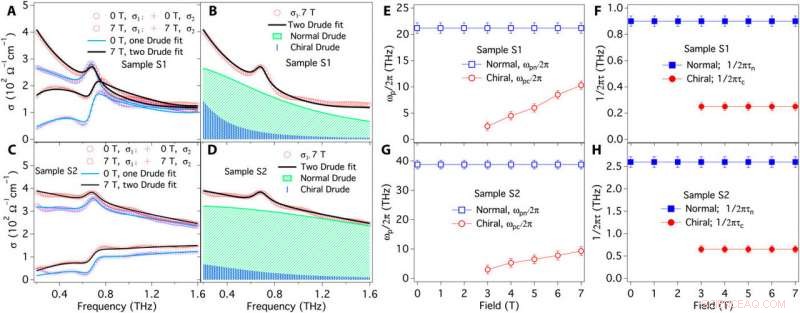
O bombeamento de carga dinâmica e relaxamento da anomalia quiral extraída por Drude-Lorentz se encaixa. (A e B) Se encaixa na condutividade terahertz da amostra S1 com ETHz ∥ B. O oscilador Drude mais nítido (área sombreada em azul) representa o novo canal de transporte da anomalia quiral. (C e D) Se encaixa na condutividade terahertz da amostra S2 com ETHz ∥ B. Frequência de plasma Drude dependente do campo na amostra S1 (E) e na amostra S2 (G). As frequências de plasma do canal de transporte quiral (ωpc / 2π, vermelho) correspondem diretamente ao bombeamento de carga quiral e são funções lineares de campo. Taxas de dispersão na amostra S1 (F) e na amostra S2 (H). As taxas de espalhamento quiral (1 / 2πτc, vermelho) controlar o processo dinâmico de anomalia quiral, como mostrado na Fig. 1D, e em ambas as amostras, eles são muito menores do que as taxas de espalhamento em massa normais (1 / 2πτn, azul). Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
Panorama
Desta maneira, Bing Cheng e colegas observaram um efeito anômalo de magnetocondutividade de terahertz no arsenieto de cádmio semimetal de Dirac. O efeito dependia do efeito magnético quiral. A dependência observada e a evolução da forma funcional da condutividade estavam de acordo com a teoria da anomalia quiral. Contudo, as taxas de espalhamento quiral e espalhamento intranodo não estavam precisamente de acordo com a teoria prevalecente, uma vez que o espalhamento quiral era muito mais forte do que o previsto. Os pesquisadores, portanto, desenvolverão modelos mais revisados com taxas mais realistas de dispersão experimental de impurezas no futuro.
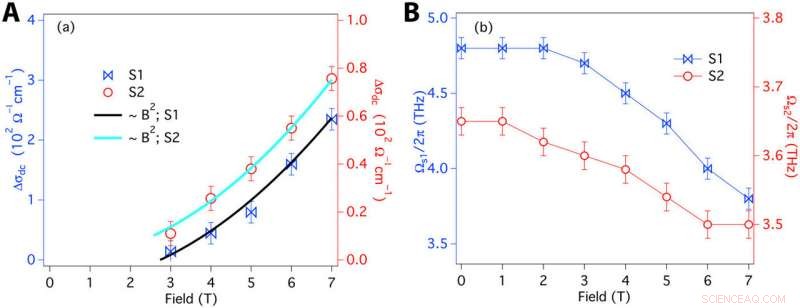
Condutividade quiral dc intrínseca extrapolada da condutividade terahertz. (A) magnetocondutividade dc intrínseca da anomalia quiral na amostra S1 (azul) e na amostra S2 (vermelho). Em ambas as amostras, Δσ segue B2, consistente com a previsão da dependência de campo da corrente quiral em regime de transporte semiclássico. (B) Força do oscilador do fone de ouvido na amostra S1 (azul) e na amostra S2 (vermelha). As intensidades do oscilador em ambas as amostras diminuem à medida que a condutividade quiral é aumentada pelo campo magnético. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
© 2021 Science X Network