
Figura 1. O perfil de intensidade espacial de um feixe de laser propagando-se em um meio não linear torna-se espontaneamente não uniforme devido ao processo de instabilidade modulacional. Crédito:Institute for Basic Science
Estamos mais familiarizados com as quatro fases convencionais da matéria:sólida, líquido, gás, e plasma. Mudanças entre duas fases, conhecido como transições de fase, são marcados por mudanças abruptas nas propriedades do material, como densidade. Nas últimas décadas, um amplo corpo de pesquisas em física tem se dedicado a descobrir novas fases não convencionais da matéria, que normalmente surgem em temperaturas ultrabaixas ou em materiais especialmente estruturados. Fases "topológicas" exóticas exibem propriedades que só podem mudar de maneira quantizada (passo a passo), tornando-os intrinsecamente robustos contra impurezas e defeitos.
Além dos estados topológicos da matéria, fases topológicas da luz podem surgir em certos sistemas ópticos, como cristais fotônicos e matrizes de guia de ondas ópticas. Os estados topológicos da luz são de interesse, pois podem formar a base para futuras tecnologias de comunicação baseadas em luz com eficiência energética, como lasers e circuitos ópticos integrados.
Contudo, em altas intensidades, a luz pode modificar as propriedades do material subjacente. Um exemplo desse fenômeno são os danos que os lasers de alta potência podem causar nos espelhos e nas lentes. Isso, por sua vez, afeta a propagação da luz, formando um loop de feedback não linear. Os efeitos ópticos não lineares são essenciais para a operação de certos dispositivos, como lasers, mas podem levar ao surgimento de desordem da ordem em um processo conhecido como instabilidade modulacional, como mostrado na Figura 1. Compreender a interação entre topologia e não linearidade é um assunto fascinante de pesquisa em andamento.
Daniel Leykam, Aleksandra Maluckov, e Sergej Flach no Centro de Física Teórica de Sistemas Complexos (PCS) do Instituto de Ciências Básicas (IBS, Coreia do Sul), junto com seus colegas Ekaterina Smolina e Daria Smirnova do Instituto de Física Aplicada, Academia Russa de Ciências e Universidade Nacional Australiana, propuseram um novo método para caracterizar fases topológicas da luz usando instabilidades não lineares exibidas por feixes de luz brilhantes. Esta pesquisa foi publicada em Cartas de revisão física .
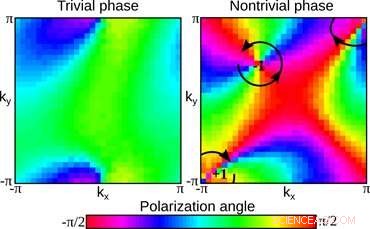
Figura 2. Perfil de polarização de campo distante de feixes de laser após o desenvolvimento da instabilidade modulacional. As fases topológicas triviais e não triviais podem ser distinguidas pela contagem do número de vórtices no ângulo de polarização. Não há vórtices na fase trivial (esquerda), e um par de vórtices de carga oposta na fase não trivial (direita). Crédito:Institute for Basic Science
Nesse trabalho, os pesquisadores abordaram a questão fundamental de como as fases topológicas da luz em meios ópticos não lineares sofrem o processo de instabilidade modulacional. Foi mostrado teoricamente que certas características da instabilidade, como sua taxa de crescimento, pode diferir entre diferentes fases topológicas. Os pesquisadores realizaram simulações numéricas da instabilidade modulacional e demonstraram que ela pode ser usada como ferramenta para identificar diferentes fases topológicas da luz. Um exemplo dessa ideia é mostrado na Figura 2:Embora os feixes de luz gerados pela instabilidade tenham padrões de intensidade aparentemente aleatórios, eles exibem uma ordem oculta em sua polarização na forma de vórtices robustos. O número de vórtices que aparecem como resultado da instabilidade é quantizado, e eles podem ser usados para distinguir diferentes fases topológicas.
A maneira mais comum de identificar fases topológicas da luz tem sido olhar para as bordas do material, onde certos comprimentos de onda ópticos se tornam localizados. Contudo, uma caracterização completa requer a medição das propriedades em massa do material, o que é uma tarefa muito mais difícil. A luz no material a granel sofre interferência de onda complicada e é altamente sensível a defeitos, que obscurece suas propriedades topológicas. Contra-intuitivamente, os pesquisadores mostraram como as instabilidades não lineares podem ser usadas para domar essa interferência indesejada e codificar espontaneamente as propriedades topológicas do material em feixes de luz. Essa abordagem fornece uma maneira mais simples de sondar e talvez até mesmo gerar estados topológicos de luz.
A próxima etapa será testar essa proposta em um experimento. Por exemplo, matrizes de guia de ondas ópticas inscritas em um vidro serão uma plataforma ideal para esse propósito. Ao iluminar o vidro com um feixe de laser pulsado brilhante, deve ser possível observar diretamente a instabilidade modulacional e, assim, medir as propriedades topológicas da matriz de guia de ondas. O grupo de pesquisa está atualmente discutindo com os colaboradores possíveis projetos para a verificação experimental de sua teoria.