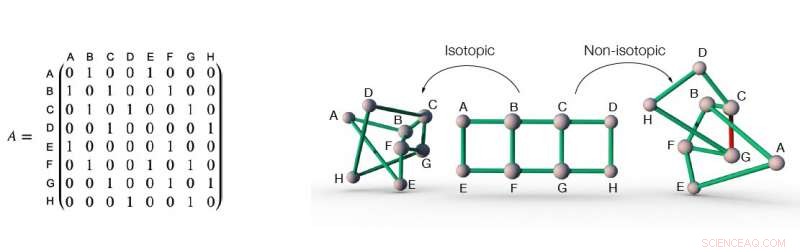
A matriz de adjacência de uma rede (esquerda), e três embeddings diferentes desta rede no espaço (direita). A matriz de adjacência de uma rede registra informações da conectividade da rede. Por exemplo, na rede da figura, os nós A e B estão conectados por um link, portanto, o elemento na matriz de adjacência na interseção da linha A e coluna B é um. De forma similar, os nós A e C não estão conectados por um link, portanto, o elemento na matriz de adjacência na interseção da linha A e coluna C é zero. Os dois primeiros embeddings de rede descritos pela matriz de adjacência à esquerda são isotópicos entre si, porque eles podem ser transformados um no outro simplesmente "achatando" a incorporação, sem a necessidade de cortar qualquer link aberto. Por outro lado, o embedding à direita não é isotópico aos outros dois embeddings, porque para transformá-lo nos outros dois, pelo menos um link (o link vermelho, por exemplo) precisa ser aberto para permitir a passagem de outro (s) link (s). Crédito:Liu, Dehmamy &Barabási.
A estrutura e funções de muitas redes físicas, incluindo o cérebro humano, o sistema vascular e outras redes biológicas, muitas vezes dependem de seu layout tridimensional e geométrico. Distinguir entre redes físicas com conexões idênticas, mas diferentes layouts geométricos, Contudo, pode ser muito desafiador.
Pesquisadores da Northeastern University introduziram recentemente uma construção teórica chamada isotopia de rede, que pode ajudar os cientistas a diferenciar entre redes físicas. A isotopia de rede oferece uma ferramenta de classificação que descreve classes de layouts de rede 3-D que podem ser transformados uns nos outros sem cruzamentos de link.
"Nosso projeto começou como uma curiosidade sobre layouts de rede, "Yanchen Liu, um dos pesquisadores que realizou o estudo, disse a Phys.org. "Existem muitas redes impressas em 3D em nosso escritório que foram estudadas em vários projetos no laboratório. Ao olhar para essas redes, nos perguntamos:Se para uma determinada rede (fiação fixa dos links) existem infinitas maneiras de colocar os nós e links no espaço 3-D, como podemos saber se dois layouts da mesma rede são iguais ou diferentes? Além disso, como devemos definir as semelhanças entre os layouts de rede e se dois layouts são diferentes, como devemos medir o nível de diferença entre eles? "
Pouco depois de começarem a conduzir suas pesquisas, Liu e seus colegas perceberam que existem duas maneiras principais em que os layouts geométricos de rede podem diferir um do outro. A primeira delas depende da extensão em que o layout de uma rede é esticado, enquanto o segundo resulta do chamado cruzamento de links (ou seja, links passando um pelo outro).
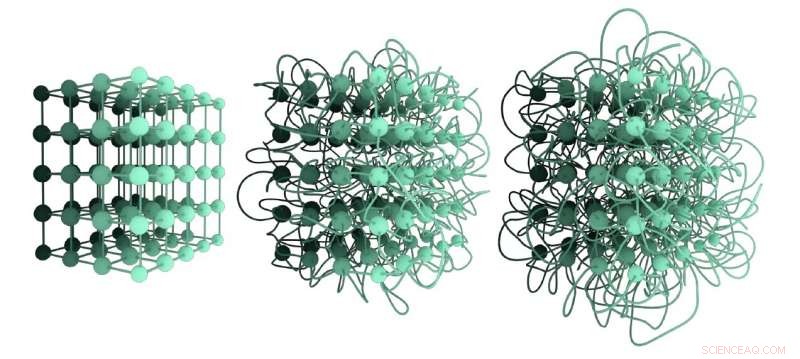
Três embeddings não isotópicos diferentes da mesma rede de rede. A incorporação à esquerda está desembaraçada; a incorporação no meio é mais emaranhada em comparação com a primeira, e a terceira incorporação é a mais emaranhada. Seu nível de emaranhamento pode ser quantificado pelo Graph Linking Number. Crédito:Liu, Dehmamy &Barabási.
"O primeiro tipo de diferença é trivial, mas o segundo tipo de diferença é intrigante, "Liu explicou." Questões semelhantes foram estudadas na teoria do nó, que é um campo dedicado a nós formados por uma ou mais curvas fechadas. "
A incorporação de uma rede física (ou seja, layout) é essencialmente uma descrição de como seus nós e links são reunidos no espaço. Em seu jornal, Liu e seus colegas introduziram um conceito chamado isotopia de incorporação de rede, que pode ser usado para distinguir entre diferentes embeddings possíveis de uma determinada rede no espaço 3-D.
"Se dois embeddings de rede são isotópicos um do outro, isso significa que eles podem ser esticados um no outro sem ter que cortar qualquer link aberto para permitir que outros links passem, "Liu disse." Por outro lado, se dois embeddings de rede não forem isotópicos entre si, isso significa que eles nunca podem ser transformados continuamente um no outro sem cortar os links. "
A noção de isotopia de rede, conforme definido por esta equipe de pesquisadores, pode ser usado para medir a extensão em que diferentes embeddings de rede estão emaranhados, uma medida conhecida como o número de ligação do gráfico. Interessantemente, Liu e seus colegas descobriram que essa medida também está correlacionada com a energia elástica de um layout.
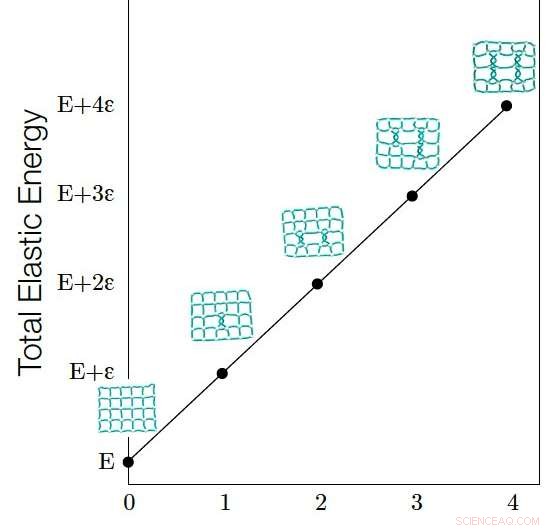
Observa-se que a energia elástica (E) de uma incorporação de rede está linearmente correlacionada ao seu Graph Linking Number (G). A energia elástica de uma incorporação de rede é proporcional ao comprimento total de todos os links. A relação linear entre E e G pode ser explicada pelo fato de que cada aumento em G estica os links na incorporação da rede, que por sua vez aumenta E, e a quantidade de aumento de energia causado por cada emaranhado (cada emaranhado faz com que G aumente em um) é quantizado e uma constante. Crédito:Liu, Dehmamy &Barabási.
Muitos sistemas físicos podem ser descritos como redes, uma parte significativa das quais são redes físicas. Os conceitos teóricos introduzidos pelos pesquisadores são ferramentas eficazes para estudar as propriedades e características geométricas desses sistemas.
"Existem três conquistas importantes neste artigo, Na minha opinião, "Liu disse." O primeiro é que definimos a isotopia de incorporação de rede, que é uma extensão da isotopia do nó da teoria do nó para embeddings de rede. A segunda é que inventamos o número de ligação do gráfico, uma medida útil do nível de emaranhamento de embeddings de rede. Finalmente, descobrimos que o número de ligação do gráfico de uma incorporação de rede está correlacionado com a energia elástica dessa incorporação de rede. "
Liu e seus colegas usaram suas descobertas para desenvolver um modelo estatístico que descreve a formação de emaranhados em uma rede física. No futuro, este modelo pode ser usado para avaliar até que ponto o layout 3-D de um sistema físico está emaranhado.
Em seu artigo recente, por exemplo, os pesquisadores usaram para examinar o emaranhado de muitos sistemas físicos, incluindo o cérebro do rato. Como todos os construtos teóricos introduzidos neste artigo podem ser aplicados a uma ampla variedade de redes físicas, eles poderiam, em última análise, apoiar pesquisas em física com foco em uma ampla gama de tópicos.
"Estamos agora continuando o estudo de redes físicas, "Liu disse." Atualmente, Estou trabalhando em uma rede física específica:a rede cerebral de larvas da mosca-das-frutas, que é uma rede formada por neurônios embutidos no espaço 3-D. Estamos especificamente interessados nas conexões entre a fisicalidade desta rede (sua incorporação) e suas propriedades estruturais (como os neurônios são conectados por meio de fiações neuronais). "
© 2020 Science X Network