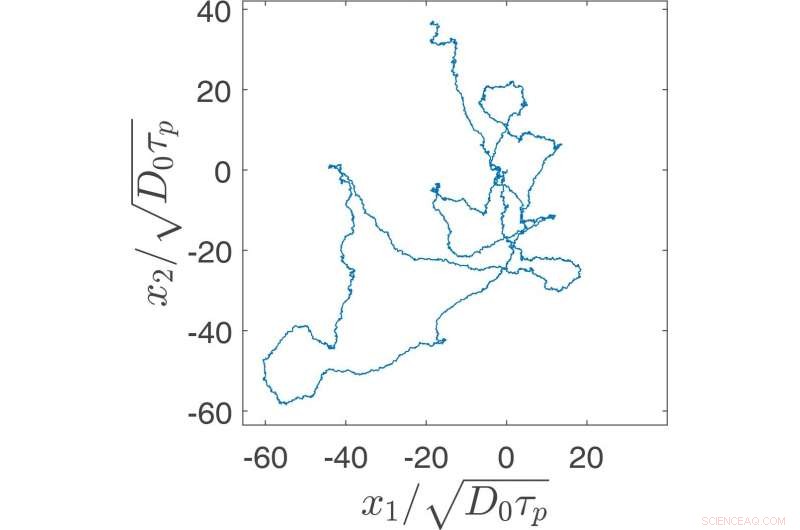
Desviando do movimento browniano. Crédito:SciencePOD
Em circunstâncias normais, as partículas seguirão movimentos aleatórios bem estabelecidos à medida que se difundem através de líquidos e gases. No entanto, em alguns tipos de sistema, esse comportamento pode ser interrompido - o que significa que os movimentos de difusão das partículas não são mais influenciados pelos resultados de cadeias de eventos anteriores. Por meio de pesquisas publicadas em EPJ E , Bernhard Mitterwallner, um Ph.D. aluno da equipe de Roland Netz da Universidade Livre de Berlim, Alemanha, desenvolveu novas teorias detalhando como essas dinâmicas incomuns podem ser reproduzidas em modelos matemáticos generalizados.
A abordagem da equipe pode permitir que os pesquisadores aprendam mais sobre comportamentos, incluindo o transporte de células biológicas, e os movimentos de materiais 'ativos' - cujas partículas coletam energia em seus ambientes circundantes para se impulsionar para a frente. Tipicamente, essas características de difusão aparecem apenas brevemente como uma transição de sistemas entre estados estáveis, mas sob as condições certas, eles podem persistir em escalas de tempo muito mais longas. Os pesquisadores podem estudar esse efeito, introduzindo um "termo de memória" em seus cálculos, que pode explicar as influências de eventos passados em diferentes escalas de tempo. Vários estudos já usaram esse princípio para explorar como esse 'movimento persistente transiente' pode ser capturado em modelos de mídia viscoelástica - que podem resistir à deformação quando a tensão é aplicada.
Os autores adotaram uma abordagem mais geral em seu estudo; baseando seus cálculos em torno de uma equação de movimento que ofereceu uma estrutura útil para descrever comportamentos de difusão não convencionais. Ao adicionar um termo de memória na equação, seus modelos dão origem ao movimento persistente transiente em uma variedade de sistemas diferentes, que não havia sido explorado em estudos anteriores. Os resultados da equipe agora podem permitir aos pesquisadores modelar com precisão os comportamentos de difusão em uma ampla gama de situações - e podem ser particularmente úteis para estudos de materiais avançados que respondem aos seus ambientes circundantes.