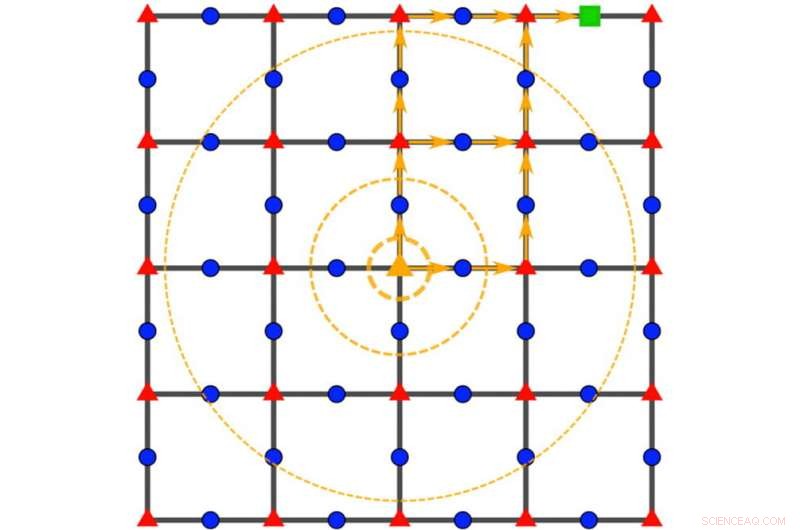
Um gráfico de comutatividade de Wang-Hazzard captura os detalhes microscópicos das funções matemáticas que os físicos normalmente usam para descrever a energia em sistemas quânticos, reduzindo o cálculo dos limites de velocidade quântica a uma equação com apenas duas entradas. Crédito:Zhiyuan Wang / Rice University
Os limites de velocidade da natureza não são colocados em placas de trânsito, mas os físicos da Rice University descobriram uma nova maneira de deduzi-los que é melhor - infinitamente melhor, em alguns casos - do que os métodos anteriores.
"A grande questão é, 'Quão rápido pode qualquer coisa - informação, massa, energia - mover-se na natureza? '"disse Kaden Hazzard, um físico quântico teórico em Rice. "Acontece que se alguém lhe entrega um material, é incrivelmente difícil, em geral, para responder à pergunta. "
Em um estudo publicado hoje na revista American Physical Society PRX Quantum , Zhiyuan Wang, estudante de pós-graduação de Hazzard e Rice, descreve um novo método para calcular o limite superior dos limites de velocidade na matéria quântica.
"Em um nível fundamental, esses limites são muito melhores do que o que estava disponível anteriormente, "disse Hazzard, professor assistente de física e astronomia e membro do Rice Center for Quantum Materials. "Este método freqüentemente produz limites que são 10 vezes mais precisos, e não é incomum que sejam 100 vezes mais precisos. Em alguns casos, a melhoria é tão dramática que encontramos limites de velocidade finitos onde as abordagens anteriores previam limites infinitos. "
O limite máximo de velocidade da natureza é a velocidade da luz, mas em quase todos os assuntos ao nosso redor, a velocidade da energia e da informação é muito mais lenta. Freqüentemente, é impossível descrever essa velocidade sem levar em conta o grande papel dos efeitos quânticos.
Na década de 1970, os físicos provaram que a informação deve se mover muito mais devagar do que a velocidade da luz em materiais quânticos, e embora eles não pudessem calcular uma solução exata para as velocidades, os físicos Elliott Lieb e Derek Robinson foram os pioneiros nos métodos matemáticos para calcular os limites superiores dessas velocidades.
"A ideia é que, mesmo que eu não possa dizer a velocidade máxima exata, posso te dizer que a velocidade máxima deve ser menor que um determinado valor, "Hazzard disse." Se eu puder dar uma garantia de 100% de que o valor real é menor do que o limite superior, isso pode ser extremamente útil. "
Hazzard disse que os físicos sabem há muito tempo que alguns dos limites produzidos pelo método Lieb-Robinson são "ridiculamente imprecisos".
"Pode-se dizer que a informação deve se mover menos de 100 milhas por hora em um material quando a velocidade real foi medida a 0,01 milhas por hora, "disse ele." Não é errado, mas não é muito útil. "
Os limites mais precisos descritos no artigo PRX Quantum foram calculados por um método criado por Wang.
"Nós inventamos uma nova ferramenta gráfica que nos permite explicar as interações microscópicas no material, em vez de depender apenas de propriedades mais grosseiras, como sua estrutura de rede, "Disse Wang.
Hazzard disse Wang, um estudante de graduação do terceiro ano, tem um talento incrível para sintetizar relações matemáticas e reformulá-las em novos termos.
"Quando eu verifico seus cálculos, Posso ir passo a passo, analise os cálculos e veja se eles são válidos, "Hazzard disse." Mas, para realmente descobrir como ir do ponto A ao ponto B, que conjunto de etapas deve ser executado quando há uma variedade infinita de coisas que você pode tentar em cada etapa, a criatividade é simplesmente incrível para mim. "
O método de Wang-Hazzard pode ser aplicado a qualquer material feito de partículas que se movem em uma rede discreta. Isso inclui materiais quânticos frequentemente estudados, como supercondutores de alta temperatura, materiais topológicos, férmions pesados e outros. Em cada um deles, o comportamento dos materiais surge de interações de bilhões e bilhões de partículas, cuja complexidade está além do cálculo direto.
Hazzard disse que espera que o novo método seja usado de várias maneiras.
"Além da natureza fundamental disso, pode ser útil para compreender o desempenho de computadores quânticos, em particular na compreensão de quanto tempo eles levam para resolver problemas importantes em materiais e química, " ele disse.
Hazzard disse estar certo de que o método também será usado para desenvolver algoritmos numéricos porque Wang mostrou que pode colocar limites rigorosos nos erros produzidos por técnicas numéricas frequentemente usadas que aproximam o comportamento de grandes sistemas.
Uma técnica popular que os físicos têm usado há mais de 60 anos é aproximar um sistema grande de um pequeno que pode ser simulado por um computador.
"Desenhamos uma pequena caixa em torno de um pedaço finito, simule isso e espero que seja o suficiente para aproximar o sistema gigantesco, "Hazzard disse." Mas não houve uma maneira rigorosa de limitar os erros nessas aproximações. "
O método Wang-Hazzard de cálculo de limites pode levar exatamente a isso.
“Existe uma relação intrínseca entre o erro de um algoritmo numérico e a velocidade de propagação da informação, "Wang explicou, usando o som de sua voz e as paredes de seu quarto para ilustrar o link.
"O pedaço finito tem arestas, assim como meu quarto tem paredes. Quando eu falo, o som será refletido pela parede e ecoará de volta para mim. Em um sistema infinito, não há limite, então não há eco. "
Em algoritmos numéricos, erros são o equivalente matemático de ecos. Eles reverberam das bordas da caixa finita, e a reflexão mina a capacidade dos algoritmos de simular o caso infinito. Quanto mais rápido a informação se move através do sistema finito, quanto menor o tempo em que o algoritmo representa fielmente o infinito.
Hazzard disse que ele, Wang e outros em seu grupo de pesquisa estão usando seu método para criar algoritmos numéricos com barras de erro garantidas.
"Nem mesmo precisamos mudar os algoritmos existentes para colocar estritos, barras de erro garantidas nos cálculos, "ele disse." Mas você também pode inverter e usar isso para fazer melhores algoritmos numéricos. Estamos explorando isso, e outras pessoas também estão interessadas em usá-los. "