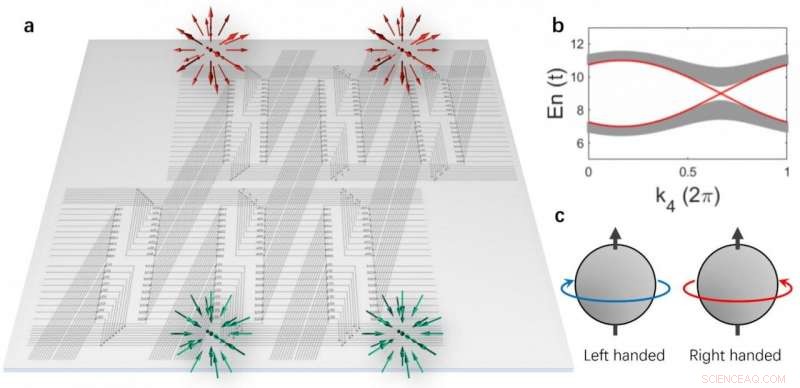
(a) A rede do circuito 4D realizada em um plano 2D. Um par de pontos Weyl com a mesma quiralidade está localizado na fronteira tridimensional. (b) As estruturas de banda em massa e os estados de Weyl de limite (linhas vermelhas). (c) Esquema da quiralidade dos estados de Weyl. Crédito:Science China Press
Nos últimos anos, a topologia surgiu como uma ferramenta importante para classificar e caracterizar propriedades de materiais. Foi descoberto que muitos materiais exibem uma série de propriedades topológicas incomuns, que não são afetados por deformações, por exemplo., alongamento, comprimindo, ou torção. Essas propriedades topológicas incluem correntes Hall quantizadas, grande magnetorresistência, e excitações de superfície que são imunes à desordem. Espera-se que essas propriedades possam ser utilizadas para tecnologias futuras, tal como, eletrônicos de baixa potência, detectores ultrarrápidos, conversores de energia de alta eficiência, ou para computação quântica.
Mais recentemente, topologia foi aplicada também a materiais sintéticos, por exemplo., cristais fotônicos ou redes de circuitos elétricos. Esses materiais sintéticos têm vários benefícios em comparação com suas contrapartes naturais. Por exemplo, a topologia de suas excitações (ou seja, suas bandas de excitação) podem ser precisamente controladas e manipuladas. Além disso, devido à sua conectividade de rede de longo alcance, materiais sintéticos podem realizar excitações topológicas em dimensões maiores do que três. Portanto, materiais sintéticos, e, em particular, redes de circuitos elétricos, oferecem a possibilidade de realizar uma série de propriedades topológicas interessantes que não são acessíveis em materiais reais.
Rui Yu da Universidade de Wuhan, Yuxin Zhao da Universidade de Nanjing, e Andreas Schnyder do Max-Planck-Institute Stuttgart agora demonstraram esse potencial construindo explicitamente uma rede de circuito elétrico que simula um isolador topológico quadridimensional (4-D) com uma simetria de reversão de tempo clássica [Fig. 1 (a)]. Isoladores topológicos são materiais que isolam no volume a granel, mas altamente condutor na superfície, devido às excitações de superfície sem intervalos. De forma similar, o isolador topológico 4-D simulado tem uma lacuna de excitação no volume a granel, dentro do qual existe um par de excitações de superfície [Fig. 1 (b)].
Essas excitações de superfície 3-D têm uma dispersão linear, e mais interessante, eles são do tipo Weyl com a mesma destreza, ou seja, eles têm graus de liberdade internos que estão girando seguindo a mesma regra da mão esquerda ou direita com relação à sua direção de propagação [Fig. 1 (c)]. Eles são de origem topológica e são diferentes de qualquer excitação de superfície encontrada em materiais convencionais. A topologia determina que essas excitações 3-D Weyl devem vir em pares e que são robustas a desordem e deformações. Os autores realizaram simulações numéricas detalhadas da rede de circuitos topológicos e mostraram que as excitações 3-D de Weyl podem ser prontamente observadas em medições dependentes de frequência.
O trabalho dos autores demonstra que as excitações topológicas podem ser facilmente realizadas em placas de circuito comercialmente disponíveis ou wafers de circuito integrado compostos de indutores e capacitores. Ele abre caminho para a realização de tipos arbitrários de excitações de superfície topológica, por exemplo, as chamadas excitações de Dirac ou Majorana de dimensões dois, três, ou ainda mais alto. A implementação do circuito elétrico de excitações topológicas tem a vantagem de ser simples, facilmente reconfigurável, e permitindo um alto grau de controle. Isso tornará possível estudar nas futuras transições de fase topológica, efeitos não lineares, fenômenos fora de equilíbrio, e sistemas abertos quânticos (por exemplo, sistemas não Hermitianos).