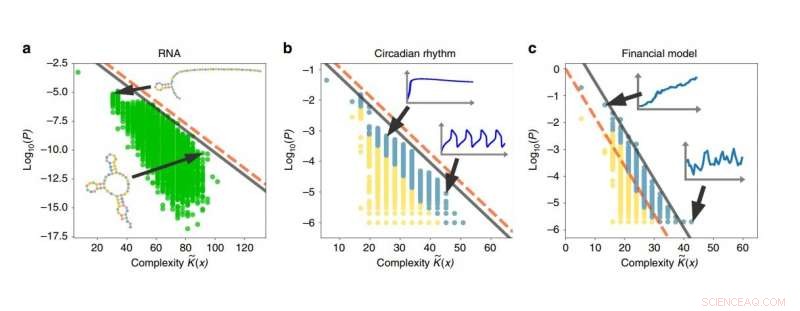
Exemplos de viés de simplicidade em sequências de RNA, ritmos circadianos, e modelos financeiros. Quanto maior a complexidade de uma saída, quanto menor a probabilidade de que a saída seja gerada. Crédito:Dingle, et al. Publicado em Nature Communications
Os pesquisadores descobriram que os mapas de entrada e saída, que são amplamente usados em ciência e engenharia para modelar sistemas que variam da física às finanças, são fortemente enviesados para a produção de resultados simples. Os resultados são surpreendentes, como ingenuamente, não há razão para suspeitar que uma saída seja mais provável do que qualquer outra.
Os pesquisadores, Kamaludin Dingle, Chico Q. Camargo, e Ard A. Louis, na University of Oxford e na Gulf University for Science and Technology, publicaram um artigo sobre seus resultados em uma edição recente da Nature Communications .
"O maior significado de nosso trabalho é nossa previsão de que o viés de simplicidade - que saídas simples são exponencialmente mais prováveis de serem geradas do que saídas complexas - vale para uma ampla variedade de sistemas em ciência e engenharia, "Louis disse Phys.org . "O viés de simplicidade implica que, para um sistema feito de muitas partes interativas diferentes - digamos, um circuito com muitos componentes, uma rede com muitas reações químicas, etc. — a maioria das combinações de parâmetros e entradas deve resultar em um comportamento simples. "
O trabalho vem do campo da teoria da informação algorítmica (AIT), que trata das conexões entre a ciência da computação e a teoria da informação. Um resultado importante do AIT é o teorema da codificação. De acordo com este teorema, quando uma máquina de Turing universal (um dispositivo de computação abstrato que pode computar qualquer função) recebe uma entrada aleatória, saídas simples têm uma probabilidade exponencialmente maior de serem geradas do que saídas complexas. Como explicam os pesquisadores, esse resultado está em total desacordo com a expectativa ingênua de que todas as saídas são igualmente prováveis.
Apesar dessas descobertas intrigantes, até agora, o teorema da codificação raramente foi aplicado a quaisquer sistemas do mundo real. Isso ocorre porque o teorema só foi formulado de uma forma muito abstrata, e um de seus principais componentes - uma medida de complexidade chamada complexidade de Kolmogorov - é incomputável.
"O teorema de codificação de Solomonoff e Levin é um resultado notável que deveria ser conhecido muito mais amplamente, "Louis disse." Ele prevê que as saídas de baixa complexidade são exponencialmente mais prováveis de serem geradas por uma máquina de Turing universal (UTM) do que as saídas de alta complexidade. Uma vez que qualquer coisa que é computável pode ser calculada em um UTM, essa é uma previsão incrível!
"Contudo, o teorema da codificação permaneceu obscuro porque UTMs são bastante abstratos, porque só pode ser provado que se mantém no limite assintótico de grandes complexidades, e porque a medida de Kolmogorov usada para determinar a complexidade é fundamentalmente incomputável. Nosso trabalho contorna esses problemas usando uma versão um pouco mais fraca do teorema da codificação que é muito mais fácil de aplicar. "
No novo, versão mais fraca do teorema da codificação, os pesquisadores substituíram a complexidade de Kolmogorov por uma complexidade de aproximação, que é computável, ao mesmo tempo que preserva a preferência exponencial pela simplicidade. O teorema da codificação mais fraco pode ser prontamente aplicado para fazer previsões sobre sistemas práticos.
"Usamos a linguagem dos mapas de entrada e saída, que pode soar um tanto abstrato, "Louis disse." No entanto, muitos sistemas estudados em ciência e engenharia convertem algum tipo de entrada em algum tipo de saída por meio de um algoritmo. Por exemplo, a informação codificada no DNA de um organismo (seu genótipo) pode ser vista como entrada, enquanto as características e o comportamento do organismo (seu fenótipo) podem ser vistos como a saída. Em um conjunto de equações diferenciais, a entrada são os parâmetros das equações, e a saída é a solução dessas equações, dadas algumas condições de contorno.
"Argumentamos que, se você escolher parâmetros de entrada aleatoriamente, então, tais sistemas são exponencialmente mais propensos a produzir resultados simples do que produtos complexos. Uma vez que essa previsão se aplica a uma ampla gama de mapas, estamos fazendo uma ampla reivindicação. Mas esse é um de seus pontos fortes. Nossa derivação não requer muito conhecimento sobre como o mapa (ou o algoritmo) em questão realmente funciona.
"Portanto, o principal significado do nosso trabalho é que nossa versão mais fraca do teorema da codificação mantém aproximadamente o viés exponencial em direção à simplicidade do teorema da codificação original, mas é muito mais fácil de aplicar na prática. "
Uma consequência dos resultados é que é possível prever a probabilidade de qualquer resultado específico com base em sua complexidade. Embora uma saída simples seja exponencialmente mais provável de aparecer do que uma saída complexa, os pesquisadores observam que isso não significa necessariamente que saídas simples são mais prováveis de aparecer do que saídas complexas em geral, uma vez que pode haver muitas saídas mais complexas do que as simples em geral.
Para ilustrar algumas aplicações, os pesquisadores usaram o teorema de codificação modificado para analisar sistemas de sequências de RNA, ritmos circadianos, e mercados financeiros, e mostrou que todos esses sistemas exibem o viés da simplicidade. No futuro, eles também planejam aplicar os resultados a algoritmos de computador, evolução biológica, e sistemas caóticos. Contudo, para uma explicação mais intuitiva do que significa viés de simplicidade, os pesquisadores descrevem um cenário envolvendo nossos parentes primatas:
"Considere o conhecido problema de macacos digitando em uma máquina de escrever, "Louis disse." Se os macacos digitarem de uma forma verdadeiramente aleatória, e a máquina de escrever tem N chaves, então a probabilidade de obter uma sequência particular de comprimento k é apenas 1 / N k , uma vez que existe um 1 / N chance de obter a tecla correta em cada um dos k degraus. Assim, cada sequência de comprimento k é igualmente provável ou improvável.
"Agora considere o caso em que os macacos estão digitando em um programa de computador. Eles podem, então, digitar acidentalmente um programa curto que gera uma saída longa. Por exemplo, há um código de 133 caracteres na linguagem de programação C que gera corretamente os primeiros 15, 000 dígitos de π. Então, em vez de 1 / N 15, 000 , que é a probabilidade dos macacos acertarem na máquina de escrever, as chances são muito menores, apenas 1/ N 133 , que os macacos geram π no computador.
Acontece que a maioria dos números não tem programas curtos que os geram, então, o melhor que os macacos no computador podem fazer para esses números é digitar um programa como 'imprimir número, 'que é quase a probabilidade de que eles acertassem em uma máquina de escrever de qualquer maneira. Mas para resultados simples, a probabilidade é muito maior do que para a máquina de escrever. Por definição, saídas simples são definidas como aquelas que têm programas curtos que as descrevem, e saídas complexas são aquelas que só podem ser descritas por programas longos. Então π é, por definição, um número com baixa complexidade, e, portanto, é muito mais provável que seja gerado por macacos digitando em um programa de computador do que muitos outros números que não são simples.
"O que o teorema da codificação faz é tornar essa história intuitiva quantitativa. Programas curtos são mais propensos a serem digitados ao acaso, e uma vez que as probabilidades de comprimento k programas também escalam como 1 / N k , saídas simples são exponencialmente muito mais prováveis de aparecer do que complexas. Nossa contribuição é demonstrar como calcular facilmente a relação exponencial entre probabilidade e complexidade para muitos sistemas práticos. O que é bom é que você não precisa saber muito sobre o mapa (ou, de forma equivalente, o algoritmo) para descobrir se uma saída provavelmente aparecerá ou não. Para uma boa primeira aproximação, quanto mais compressível é uma saída, o mais provável é que apareça em entradas aleatórias. "
© 2018 Phys.org