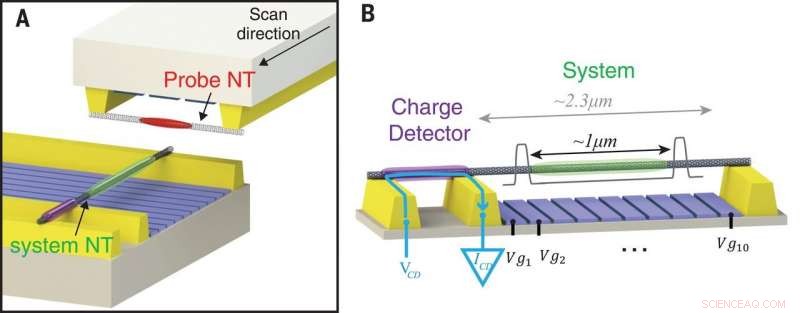
Plataforma experimental para geração de imagens de elétrons com forte interação. (A) Configuração da sonda de varredura que consiste em dois dispositivos de nanotubos de carbono (NT) - um dispositivo NT do sistema (parte inferior) que hospeda os elétrons a serem visualizados (elipse verde) e um dispositivo NT da sonda (parte superior) contendo os elétrons de sondagem (vermelho ) No experimento, o NT da sonda é varrido junto com o NT do sistema (seta preta). (B) O sistema NT está conectado aos contatos (amarelo) e está suspenso acima de 10 portas (azul) usado para criar um poço de potencial (mostrado esquematicamente em cinza) que confina alguns elétrons à parte do meio do NT suspenso (verde) , longe dos contatos. A adição desses elétrons é detectada usando um detector de carga - um ponto quântico separado formado em um segmento lateral do mesmo NT (roxo). O detector é polarizado por uma tensão, VCD, aplicado em um contato externo, levando a uma corrente, ICD, fluindo apenas entre os contatos do detector de carga (seta azul), de forma que nenhuma corrente passe pela parte principal do sistema NT. Crédito:Ciência, doi:10.1126 / science.aat0905
Quando os elétrons que se repelem estão confinados a um pequeno espaço, eles podem formar um estado cristalino ordenado conhecido como cristal de Wigner. Observar o cristal frágil é complicado, uma vez que requer condições extremas, incluindo baixas temperaturas e densidades, bem como sondas de imagem não invasivas. Para superar as condições desafiadoras de imagem, I. Shapir e uma equipe de pesquisa nos departamentos de Física e Física da Matéria Condensada em Israel, Romênia e Hungria criaram condições em um nanotubo de carbono (NT) para abrigar os elétrons. Eles seguiram esta etapa experimental usando um segundo nanotubo como uma sonda (chamado de "sonda NT") para escanear o primeiro nanotubo (denominado "sistema NT"). Os físicos mediram as densidades eletrônicas e mostraram sua consistência com previsões teóricas para demonstrar pequenos cristais de Wigner de até seis elétrons em uma dimensão (1-D). Os resultados agora são publicados em Ciência .
Mais de 80 anos atrás, o físico Eugene Wigner previu o cristal quântico de elétrons, que continua sendo um dos estados da matéria mais evasivos. No presente trabalho, Shapir e colegas de trabalho desenvolveram uma técnica para obter imagens diretas do cristal de Wigner em 1-D, criando imagens de sua densidade de carga no espaço real. Eles obtiveram imagens de alguns elétrons confinados em 1-D que correspondiam às previsões teóricas para cristais de forte interação. Os cientistas viram a natureza quântica do cristal usando um túnel coletivo através de uma barreira de potencial elétrico confinada com portas eletricamente independentes. O trabalho forneceu evidências diretas para a formação de pequenos cristais de Wigner, pavimentando o caminho para estudar os estados frágeis de interação dos elétrons por meio de imagens de sua densidade de muitos corpos no espaço real.
Em seu artigo de 1934, o físico Eugene Wigner previu que, quando as interações de Coulomb de longo alcance em um sistema de elétrons dominavam a energia cinética e a desordem, eles emergiriam em um estado fundamental cristalino. Onde os elétrons foram mantidos separados independentemente de seu número quântico. Os físicos experimentais começaram a procurar por este cristal quântico nos sistemas eletrônicos mais limpos disponíveis depois disso, incluindo hélio líquido e heteroestruturas semicondutoras de baixa dimensão.
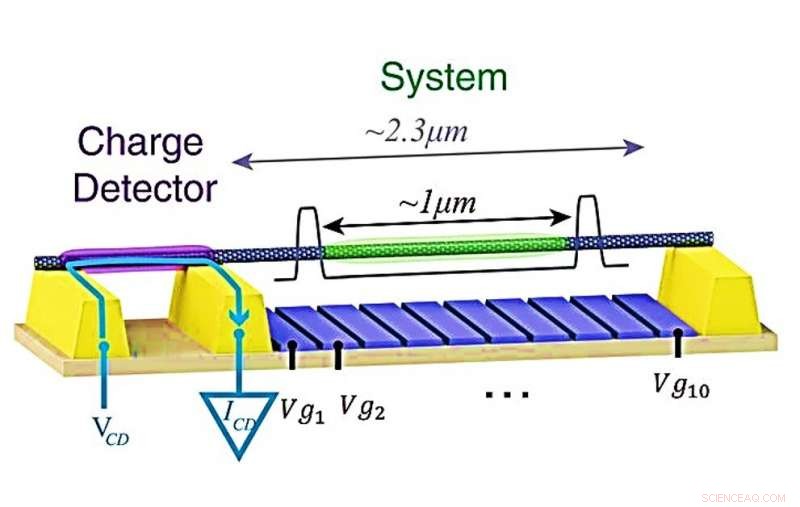
Plataforma experimental para criar imagens do cristal Wigner. O sistema NT está conectado a contatos (amarelo) e está suspenso acima de 10 portas (azul) usadas para criar um poço de potencial (mostrado esquematicamente em cinza) que confina alguns elétrons à parte média do NT suspenso (verde), longe dos contatos. A adição desses elétrons é detectada usando um detector de carga - um ponto quântico separado formado em um segmento lateral do mesmo NT (roxo). O detector é polarizado por uma tensão, VCD, aplicado em um contato externo, levando a uma corrente, ICD, fluindo apenas entre os contatos do detector de carga (seta azul), de forma que nenhuma corrente passe pela parte principal do sistema NT. Crédito:Ciência, doi:10.1126 / science.aat0905.
Os físicos já haviam realizado medições em sistemas eletrônicos bidimensionais (2-D) relativos ao transporte, campos de microondas, ressonância magnética nuclear, óptico, tunelamento e sistemas de elétrons de bicamada para indicar a existência de um cristal em campos magnéticos elevados. Observando um estado cristalino em uma dimensão (1-D), em um sistema infinito é inesperado, já que as flutuações térmicas e quânticas podem destruir a ordem de longo alcance. Contudo, em sistemas finitos, os físicos haviam estudado o estado teórico unidimensional do cristal de Wigner, uma vez que a ordem de quase-longo alcance produzia correlações cristalinas. Físicos experimentais seguiram esta observação com sondagem experimental por meio de medições de transporte, mas os experimentos só puderam sondar as propriedades macroscópicas desse estado.
Em princípio, uma ferramenta de imagem adequada é necessária para observar a impressão digital inequívoca de um cristal de Wigner em sua estrutura de espaço real. Os cientistas, portanto, usaram experimentos com sondas de varredura, embora eles pudessem apenas visualizar o estado de não interação ou mostrar portas invasivas pela sonda. As medições destacaram a dificuldade inerente de imagens de interações de elétrons com métodos convencionais de varredura. Para resolver e identificar os elétrons individualmente, um macroscópico, a ponta metálica ou dielétrica deve se aproximar dos elétrons mais perto do que sua separação mútua. No entanto, tais dicas e suas interações podem distorcer fortemente o estado que está sendo estudado. Os cientistas, portanto, precisaram de uma sonda de varredura diferente para obter imagens de um estado de interação ou sistema eletrônico.

Imagem em espaço real do perfil de densidade de um único elétron confinado. (A) Para obter imagens da distribuição de densidade de um único elétron confinado em uma "caixa" potencial (cinza), colocamos uma carga fixa no NT da sonda e a varremos no NT do sistema. Esta carga cria uma perturbação local na posição da sonda xprobe (vermelho), que muda a energia do estado fundamental do elétron do sistema, E1 (painéis superiores), proporcional à densidade local na posição da sonda E1 (xprobe) ~ ρ1 (xprobe). Medindo a tensão global da porta, Vg, necessário para manter a carga deste único elétron em ressonância com a energia Fermi dos terminais, EF, para variação de xprobe (painéis inferiores), os cientistas traçam efetivamente o perfil de sua distribuição de carga Vg (xprobe) ~ ρ1 (xprobe). (B) A derivada da corrente do detector de carga em relação a Vg, dICD / dVg, medido como uma função Vg. O pico de carga acentuado corresponde ao primeiro elétron entrando no poço de potencial do sistema NT (na Fig. 3, os rótulos verde e vermelho indicam o número de elétrons no sistema e na sonda, respectivamente). a.u., unidades arbitrárias. (C) dICD / dVg em função de Vg e xprobe. A ressonância de carga traça uma curva que dá a densidade de carga do elétron convolvido com a função de espalhamento de ponto da sonda. (Inserções) Ilustração do sistema e dispositivos de sonda para diferentes posições de medição. (D) O mesmo que em (C), mas para diferentes cargas de sonda de qprobe =0e a 3e. (E) Os traços extraídos do painel (D), tramados juntos. Crédito:Ciência, doi:10.1126 / science.aat0905.
No presente trabalho, Shapir et al. introduziu uma plataforma de sonda de varredura que usava um nanotubo de carbono (NT) como altamente sensível, ainda sonda de varredura minimamente invasiva para visualizar a densidade de muitos corpos de elétrons que interagem fortemente. A plataforma continha um microscópio de sonda de varredura feito sob medida operando em temperaturas criogênicas (~ 10 mK), onde dois dispositivos NT opostos podiam ser colocados em estreita proximidade e escaneados um ao lado do outro. Os cientistas usaram um dispositivo para hospedar o sistema NT como a plataforma 1-D em estudo, e o segundo dispositivo perpendicularmente àquele para conter a sonda NT. Eles montaram os dois dispositivos usando uma técnica de nanomontagem para formar NTs imaculados suspensos acima de uma série de portões metálicos.
Os cientistas mantiveram interações fortes e baixa desordem no sistema para obter um cristal de Wigner suspendendo os NTs muito acima dos portões metálicos em 400 nm. Em seguida, usando 10 portas eletricamente independentes, eles projetaram um potencial que confinou os elétrons entre duas barreiras de 1 µm de distância, localizando-os centralmente em um nanotubo suspenso longo, longe de contatos para evitar interações indesejáveis.
Shapir et al. usou barreiras altamente opacas para evitar a hibridização da função de onda do elétron confinado com as dos elétrons no resto do NT. Como o transporte nesta situação foi altamente suprimido, os cientistas investigaram os elétrons confinados usando um detector de carga localizado em um segmento separado do mesmo NT. O dispositivo NT da sonda usado separadamente no estudo manteve uma estrutura quase idêntica, que só diferia pelo comprimento da suspensão de 1,6 µm e pelo número de portas (três).
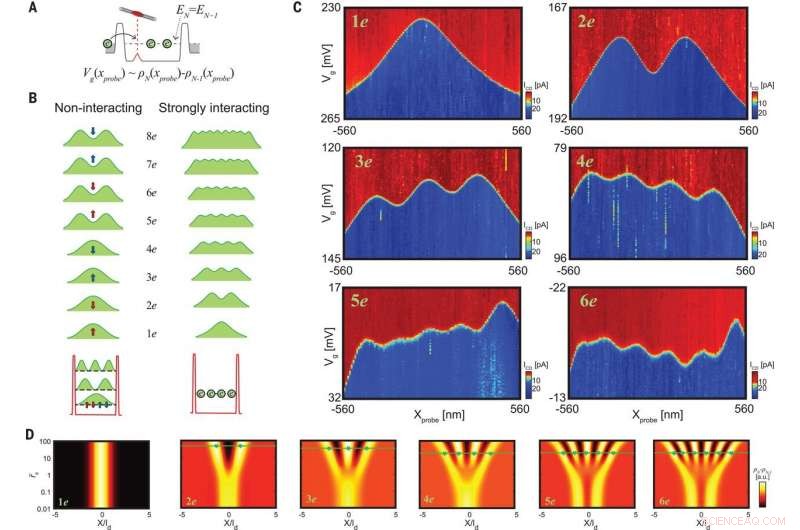
:Imagens da densidade diferencial de estados de muitos elétrons. (A) Em uma transição de carga de N - 1 para N elétrons, a ressonância ocorre para EN =EN – 1 e a mudança de tensão da porta representa a densidade diferencial Vg (xprobe) ~ ρN (xprobe) - ρN - 1 (xprobe). (B) Ilustração da densidade diferencial esperada de elétrons não interagentes (à esquerda) versus fortemente interagindo (à direita) em um NT de carbono. Esses esboços também incluem a mancha de resolução finita. Elétrons não interativos ocupam as funções de onda da partícula em uma caixa, cada um sendo quatro vezes degenerado por causa da degeneração do spin e do vale (setas vermelhas e azuis). Consequentemente, a densidade diferencial dos primeiros quatro elétrons deve ser idêntica e de pico único, e o dos próximos quatro deve ter pico duplo. Para o caso de forte interação, os elétrons se separam no espaço real (canto inferior direito), e cada elétron adicionado adicionará mais um pico ao perfil de densidade diferencial (canto superior direito). (C) Medição de ICD em função de Vg e xprobe, em torno dos picos de carga dos primeiros seis elétrons no sistema. As curvas traçam diretamente a densidade diferencial desses estados de muitos elétrons, mostrando que eles estão profundamente envolvidos no regime de interação forte. (D) A densidade diferencial dos primeiros seis elétrons, calculado com DMRG, que considera as interações eletrônicas de longo alcance como uma função da coordenada espacial x / ld e a força efetiva das interações eletrônicas, r˜s, variando de muito fraco (r˜s =0,01) a muito forte (r˜s =100). Estrelas verdes marcam as posições dos picos medidos no experimento, e as linhas verdes marcam as posições calculadas (com um único parâmetro livre ld =160 nm). Crédito:Ciência, doi:10.1126 / science.aat0905.
Os cientistas demonstraram o princípio de funcionamento subjacente à técnica de imagem conhecida como "carga de digitalização, "começando com os experimentos mais simples sobre a geração de imagens da distribuição de carga de um único elétron confinado em uma caixa 1-D. Shapir et al. mediram a resposta energética do sistema a uma perturbação digitalizada (agitação) e determinaram diretamente a distribuição de densidade do sistema. medir a energia do sistema em função da sonda NT, os cientistas resolveram diretamente o perfil de densidade do elétron. Ao medir a energia, os cientistas referiram-se à energia de Fermi nas derivações e creditaram a perturbação produzida pelas sondas à separação entre os dois NTs e à carga confinada dentro da sonda NT.
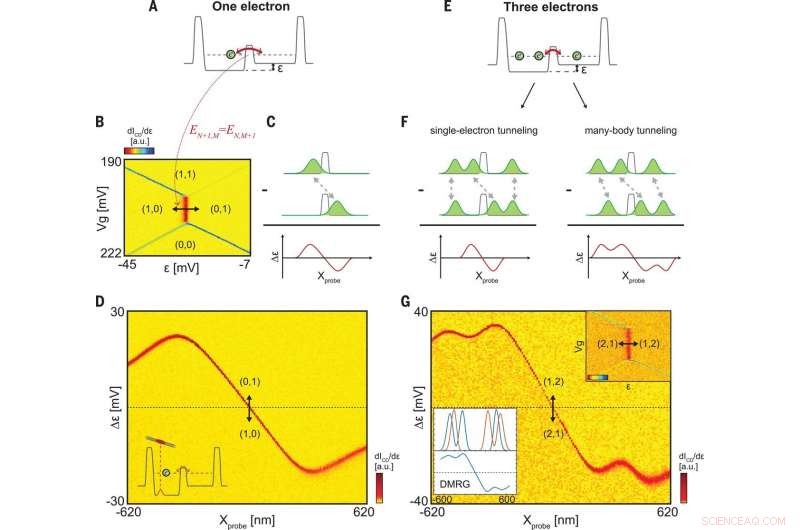
Tunelamento de vários corpos do estado de poucos elétrons. (A) Ilustração da paisagem potencial, que agora inclui uma barreira central através da qual um elétron pode criar um túnel (seta vermelha). A tensão de dessintonização, ε, altera a altura relativa do fundo de cada poço. (B) Diagrama de estabilidade de carga para 1e em função de Vg e ε, medido usando dICD / dε (barra de cores). Os estados (N, M) denotam a carga N (M) nos poços esquerdo (direito). A vertical, a linha mais larga corresponde a um túnel interno, ocorrendo quando EN + 1, M =EN, M + 1. (C) Esquema da densidade diferencial de tunelamento esperada para um elétron ("dipolo" vermelho, fundo), dada pela diferença entre sua distribuição de densidade antes e depois do tunelamento [ρ10 (x) e ρ01 (x)] convolvida com a função de propagação do ponto da sonda (PSF). (D) Sinal do detector de carga medido como uma função x sonda e a diferença na dessintonização em relação ao estado não perturbado, Δε. O traço vermelho mostra o Δε (xprobe) necessário para manter o tunelamento em ressonância (mostrado esquematicamente na inserção), dando a densidade diferencial de tunelamento. (E) O mesmo que (A), mas por três elétrons na armadilha. (F) Dois cenários para o tunelamento:(Esquerda) Apenas o elétron central se move no evento de tunelamento; Δε (xprobe) mostrará um único dipolo, como no caso de um elétron ilustrado em (C). (Certo) Tunelamento de muitos corpos, em que as coordenadas de todos os elétrons se movem coerentemente no processo de tunelamento; múltiplos dipolos são esperados no sinal de tunelamento diferencial. (G) (detalhe superior) Diagrama de estabilidade de carga de três elétrons, com ICD / dε (a.u.) medido para −42 mV <ε <10 mV, 170 mV
Shapir et al. obteve seis painéis nos experimentos para indicar a densidade diferencial dos seis elétrons adicionados ao sistema NT. Para perturbações mínimas, eles realizaram todas as varreduras com um elétron na sonda NT. Os perfis de densidade com imagens claramente diferiam daqueles previstos pela física de uma única partícula, embora correspondessem aos de um cristal de forte interação. Quando Shapir et al. aumentou o número de elétrons, o espaçamento de elétrons reduzido, embora sua velocidade geral tenha aumentado para significar elétrons confinados em uma "caixa" com paredes macias. As imagens resultantes forneceram diretamente, observações em espaço real dos cristais eletrônicos de Wigner.
Para entender quantitativamente as medições, Shapir et al. realizou cálculos de grupo de renormalização de matriz de densidade (DMRG) e incluiu interações de Coulomb de longo alcance. As posições dos elétrons medidas (vistas como estrelas verdes) concordaram bem com as preditas pelo DMRG, colocar os cristais observados bem dentro do regime de interação forte na configuração experimental. Para entender a natureza quântica do cristal de Wigner, Shapir et al. mediu as características de tunelamento do cristal e esperou que as correlações entre os elétrons em um cristal fizessem com que o cristal se tunelasse através de uma barreira coletivamente. Eles observaram que a densidade diferencial de tunelamento se tornou mais interessante em um sistema com mais de um elétron, uma vez que exibia impressões digitais diretas de movimento coletivo.
Desta maneira, Shapir et al. usou um novo método para obter imagens diretamente da ordenação espacial dos elétrons em interação. Com base nos resultados, eles antecipam a possibilidade de abordar questões básicas adicionais relacionadas ao cristal eletrônico quântico, incluindo a natureza de sua ordenação magnética. A plataforma de digitalização desenvolvida por Shapir et al. permitirá uma maior exploração de uma ampla gama de estados de elétrons em interação canônico da matéria que estavam anteriormente fora do alcance da imagem.
© 2019 Science X Network