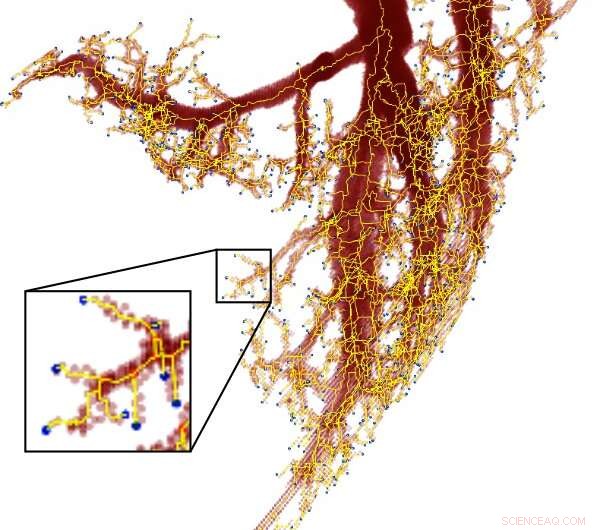
Como as veias se ramificam em divisões aproximadamente proporcionais, eles também são considerados um fractal. Crédito:Imagem de cortesia / Mitchell Newberry
Terremotos gigantescos e extrema riqueza podem não parecer ter muito em comum, mas a frequência com que o "Grande" atingirá São Francisco e a frequência com que alguém ganhará tanto dinheiro quanto Bill Gates podem ser previstas com uma medição estatística chamada expoente da lei de potência.
No último século, pesquisadores usaram o que é chamado de lei de potência para prever certos tipos de eventos, incluindo a frequência com que terremotos em certos pontos da escala Richter ocorrerão. Mas um pesquisador da Universidade de Michigan percebeu que essa lei de potência não se aplica a todas as circunstâncias.
Mitchell Newberry, um colega de Michigan e professor assistente no Centro de U-M para o Estudo de Sistemas Complexos, sugere um ajuste à lei de potência que explicaria os eventos que aumentam ou diminuem em proporções fixas - por exemplo, quando um gerente ganha cerca de 20% a mais do que seu funcionário.
Esses ajustes afetam como estimar as probabilidades de terremotos, o número de capilares do corpo humano, e os tamanhos das megacidades e explosões solares. E eles podem revisar quando esperar o próximo Grande Um.
Quando os cientistas traçam algo como a probabilidade de extrema riqueza em um gráfico, a curva é uma linha suave. Isso porque as pessoas podem ter qualquer quantia de dinheiro em suas contas bancárias.
"A suavidade desta curva significa que qualquer valor é possível, "Newberry disse." Eu poderia ganhar um centavo a mais tão facilmente quanto um centavo a menos. "
Esse não é exatamente o caso com eventos como terremotos por causa de como eles são registrados na escala Richter. A magnitude Richter dos terremotos aumenta ou diminui em incrementos de 0,1, exponencialmente. Um terremoto de magnitude 3,1 é 1,26 vezes mais poderoso que terremotos de magnitude 3,0, portanto, nem todos os valores são possíveis na escala. A escala Richter é um exemplo de um conceito chamado "auto-similaridade, "ou quando um evento ou coisa é feito de cópias proporcionalmente menores de si mesmo.
Você pode ver a auto-semelhança na natureza como a ramificação das veias de uma folha, ou em geometria como triângulos de ajuste dentro de triângulos maiores da mesma forma, chamado de triângulo de Sierpinski. Então, para contabilizar eventos que mudam em proporções exatas, Newberry e seu co-autor Van Savage, da University of California, Los Angeles, construiu a lei de potência discreta.

A curva de Koch se repete infinitamente, exibindo auto-similaridade. Crédito:usuário da Wikimedia Leofun01
Nessas equações de lei de potência, o expoente na equação é a variável para a qual os cientistas estão resolvendo. Em terremotos, aquele expoente, chamado de valor b de Gutenberg-Richter, foi medido pela primeira vez em 1944 e indica a frequência com que um terremoto de certa intensidade pode ocorrer. A lei de potência discreta de Newberry produziu uma correção de 11,7% sobre as estimativas com base na lei de potência contínua, aproximando o expoente da frequência histórica de grandes terremotos. Mesmo uma correção de 5% se traduz em uma diferença de mais de duas vezes em quando esperar o próximo terremoto gigante.
"Por 100 anos, as pessoas têm falado sobre aproximadamente um tipo de distribuição de lei de potência. É a distribuição de riqueza e terremotos da lei de potência, "Newberry disse." Só agora, estamos documentando essas escalas discretas. Em vez de uma curva suave, nossa lei de potência parece uma escada infinita. "
Newberry percebeu a falha na lei de potência contínua em seu estudo da física do sistema circulatório. O sistema circulatório começa com um grande vaso sanguíneo:a aorta. À medida que a aorta se divide em diferentes ramos - as artérias carótida e subclávia - cada novo ramo diminui de diâmetro em cerca de dois terços.
Ele estava usando a lei de potência contínua para estimar o tamanho dos vasos sanguíneos à medida que continuam a se ramificar. Mas a lei de potência revelou tamanhos de vasos sanguíneos que não podiam ocorrer. Indicou que um vaso sanguíneo pode ser apenas ligeiramente menor do que o tronco do qual se ramificou, em vez de cerca de dois terços do tamanho desse tronco.
"Usando a lei de potência contínua, estávamos apenas recebendo respostas que sabíamos que estavam erradas, "Newberry disse." Ao depurar o que falhou, descobrimos que essa distribuição pressupõe que cada tamanho de vaso sanguíneo é igualmente plausível. Nós sabemos que para vasculatura real, Esse não é o caso."
Então, Newberry fez a engenharia reversa da lei de potência. Olhando para os vasos sanguíneos, Newberry pode deduzir o expoente da lei de potência a partir de duas constantes:quantos ramos em cada junção - dois - e quanto menor cada ramo é em relação ao tronco. Medindo os tamanhos dos navios em cada divisão, Newberry conseguiu resolver a distribuição dos vasos sanguíneos.
"Há um meio-termo entre uma lei de potência contínua e a lei de potência discreta, "Newberry disse." Na lei de potência discreta, tudo está disposto em proporções perfeitamente rígidas, desde a escala mais alta até a infinitesimalmente pequena. Na lei de potência contínua, tudo está perfeitamente disposto de forma aleatória. Quase tudo que se assemelha a si mesmo na realidade é uma mistura dos dois. "
O estudo de Newberry foi publicado na revista Cartas de revisão física .