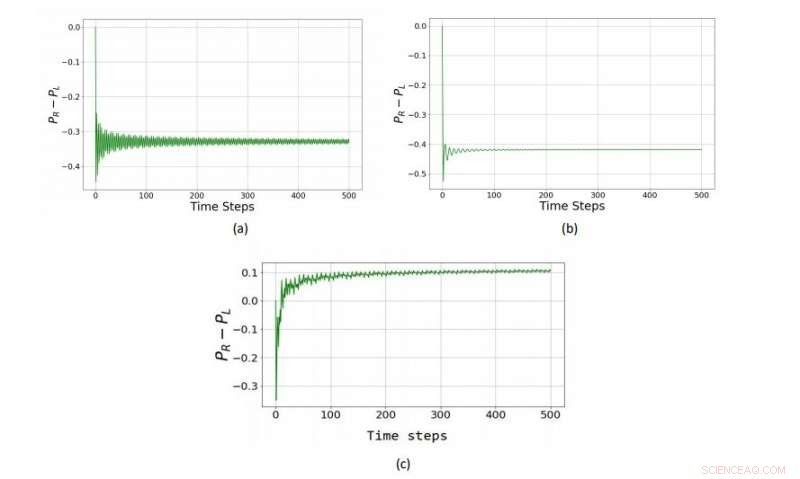
Em uma versão quântica de um jogo de Parrondo jogado com uma moeda de três estados (um qutrit), as duas estratégias perdedoras (a) e (b) são combinadas em uma estratégia vencedora (c). Crédito:Rajendran et al. © 2018 EPL
Os físicos demonstraram que o paradoxo de Parrondo - um aparente paradoxo em que duas estratégias perdedoras se combinam para formar uma estratégia vencedora - pode surgir como um jogo de moedas com uma única moeda no reino quântico, mas apenas quando a moeda tem três estados (cara, caudas, e um lado) em vez dos dois convencionais.
Em geral, Paradoxo de Parrondo, também chamado de jogo de Parrondo, só funciona quando as duas estratégias perdedoras são de alguma forma dependentes uma da outra e são combinadas de forma a mudar as condições que as levam à derrota. Desde que foi descoberto pelo físico Juan Parrondo em 1996, O paradoxo de Parrondo encontrou aplicações na engenharia, finança, e biologia evolutiva, entre outras áreas.
Uma das maneiras mais simples de implementar um jogo de Parrondo é descrita nesta entrada da Wikipedia. Suponha que você tenha $ 100, e você pode escolher jogar qualquer combinação de dois jogos. No primeiro jogo, você perde $ 1 toda vez que joga. No segundo jogo, você ganha $ 3 se tiver um número par de dólares restantes, e você perderá $ 5 se sobrar um número ímpar de dólares. Se você jogar apenas o primeiro jogo ou apenas o segundo jogo, você acabará perdendo todo o seu dinheiro, portanto, jogar cada jogo sozinho é uma estratégia perdedora. Contudo, se você alternar entre os dois jogos, começando com o segundo jogo, então você ganhará $ 2 para cada dois jogos que jogar, para que as duas estratégias perdedoras possam se combinar em uma estratégia vencedora.
No novo estudo, os físicos Jishnu Rajendran e Colin Benjamin do Instituto Nacional de Educação e Pesquisa em Ciências, HBNI, na Índia, demonstraram um jogo de Parrondo usando uma moeda de três estados, que eles representam com um qutrit, um sistema quântico com três estados.
"Os jogos de Parrondo foram vistos em um contexto clássico, "Benjamin disse Phys.org . "Nosso objetivo neste trabalho foi mostrar como implementá-lo em um contexto quântico, em particular em uma caminhada quântica. Infelizmente, a versão quântica deste jogo quando implementada com uma única moeda (qubit) em uma caminhada quântica falhou nos limites assintóticos. O que mostramos neste trabalho é que um qutrit pode implementar esse jogo de Parrondo em uma caminhada quântica. "
Na caminhada quântica, um jogador começa na origem e se move para a direita (direção positiva) ou para a esquerda (direção negativa) de acordo com o resultado do sorteio. Se cabeças, o jogador se move para a direita; se coroa, deixou; e se o resultado for "lado, "então o jogador interpreta isso como um" estado de espera "e permanece no mesmo lugar. Como o qutrit é um sistema quântico, também pode estar em uma superposição desses estados, nesse caso, o jogador se move para uma posição correspondente, em algum lugar entre uma etapa completa à esquerda ou à direita. No final do jogo, se a probabilidade de o jogador ser encontrado à direita da origem for maior do que a probabilidade de ser encontrado à esquerda da origem, o jogador vence. De outra forma, eles perderam.
Usando alguns dos métodos padrão em física de partículas para definir os conceitos de um lançamento de moeda e regras do jogo com uma superposição de estados, os físicos demonstraram vários exemplos de jogos que resultam em derrotas quando jogados individualmente, mas quando combinados em uma sequência alternada resultam em um resultado vencedor. Eles também demonstraram exemplos do contrário. Por exemplo, dois jogos que resultam em uma vitória e um empate quando jogados individualmente podem resultar em um resultado perdido quando combinados.
Os físicos também mostraram que, embora não seja possível implementar um jogo de Parrondo usando uma única moeda de dois lados (qubit), é possível implementar um jogo de Parrondo usando duas moedas de dois lados (dois qubits). Os estados adicionais fornecem essencialmente flexibilidade adicional para combinar estratégias que podem superar as condições de perda.
Dadas as amplas aplicações dos jogos clássicos de Parrondo, os físicos esperam que a versão quântica possa levar a novos insights sobre o projeto de algoritmos quânticos.
"O jogo de Parrondo é uma receita para provar que nem sempre é necessário buscar uma estratégia (ou algoritmo) vencedora em um jogo, "Benjamin disse." Classicamente, existem muitas aplicações dos jogos de Parrondo, variando desde a explicação de processos fisiológicos na célula até o aumento de nossa compreensão dos motores brownianos e até mesmo em investimentos de portfólio diversificado. Classicamente, Foi demonstrado que o paradoxo de Parrondo funciona usando passeios aleatórios clássicos.
"Implementar um jogo de Parrondo em uma caminhada quântica teria implicações para o desenvolvimento de algoritmos quânticos melhores ou mais rápidos. Um algoritmo que usa princípios quânticos como superposição e / ou emaranhamento é um algoritmo quântico. se pode ser implementado em uma caminhada quântica, seria mais lucrativo do que aquele que só pode ser implementado em um passeio aleatório clássico. Como os passeios quânticos se espalham quadraticamente mais rápido do que os passeios aleatórios clássicos, um algoritmo implementado em um passeio quântico levará muito menos tempo para ser concluído do que um em um passeio aleatório clássico. Avançar, a implementação bem-sucedida do jogo de Parrondo em uma caminhada quântica fornece uma explicação algorítmica para as catracas quânticas [sistemas que têm movimento em apenas uma direção]. "
© 2018 Phys.org