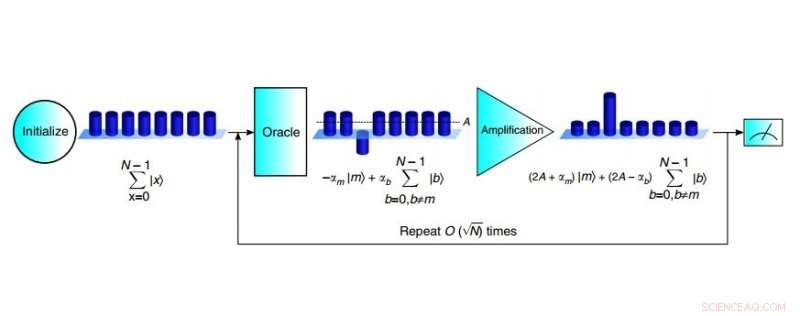
Os três estágios do algoritmo de busca de Grover de 3 qubit:inicialização, oráculo, e amplificação. Crédito:C. Figgatt et al. Publicado em Nature Communications
Pesquisando em grande, bancos de dados não ordenados para um item desejado é uma tarefa demorada para computadores clássicos, mas espera-se que os computadores quânticos realizem essas pesquisas muito mais rapidamente. Pesquisas anteriores mostraram que o algoritmo de pesquisa de Grover, proposto em 1996, é um algoritmo de busca quântica ideal, o que significa que nenhum outro algoritmo quântico pode pesquisar mais rápido. Contudo, implementar o algoritmo de Grover em um sistema quântico tem sido um desafio.
Agora em um novo estudo, pesquisadores implementaram o algoritmo de Grover com íons atômicos aprisionados. O algoritmo usa três qubits, que corresponde a um banco de dados de 8 (2 3 ) Itens. Quando usado para pesquisar no banco de dados por um ou dois itens, as probabilidades de sucesso do algoritmo de Grover eram - como esperado - significativamente mais altas do que as melhores probabilidades de sucesso teóricas para computadores clássicos.
Os pesquisadores, Caroline Figgatt et al., na Universidade de Maryland e na National Science Foundation, publicaram um artigo sobre seus resultados em uma edição recente da Nature Communications .
"Este trabalho é a primeira implementação de um algoritmo de busca de Grover de 3 qubit em um sistema de computação quântica escalável, "Figgatt disse Phys.org . "Além disso, esta é a primeira implementação do algoritmo usando oráculos booleanos, que pode ser comparada diretamente com uma pesquisa clássica. "
A abordagem clássica para pesquisar um banco de dados é direta. Basicamente, o algoritmo adivinha aleatoriamente um item, ou "solução". Então, por exemplo, para uma única iteração de pesquisa em um banco de dados de 8 itens, um algoritmo clássico faz uma consulta aleatória e, se isso falhar, faz uma segunda suposição aleatória - no total, supondo 2 de 8 itens, resultando em uma taxa de sucesso de 25%.
Algoritmo de Grover, por outro lado, primeiro inicializa o sistema em uma superposição quântica de todos os 8 estados, e então usa uma função quântica chamada oráculo para marcar a solução correta. Como resultado dessas estratégias quânticas, para uma única iteração de pesquisa em um banco de dados de 8 itens, a taxa de sucesso teórica aumenta para 78%. Com uma taxa de sucesso mais alta, os tempos de pesquisa são mais rápidos, já que menos consultas são necessárias, em média, para chegar à resposta correta.
Na implementação do algoritmo de Grover relatado aqui, a taxa de sucesso foi inferior ao valor teórico - cerca de 39% ou 44%, dependendo do oráculo usado - mas ainda marcadamente mais alto do que a taxa de sucesso clássica.
Os pesquisadores também testaram o algoritmo de Grover em bancos de dados que têm duas soluções corretas, nesse caso, as taxas de sucesso teóricas são 47% e 100% para computadores clássicos e quânticos, respectivamente. A implementação demonstrada aqui alcançou taxas de sucesso de 68% e 75% para os dois tipos de oráculo - novamente, melhor do que o valor teórico mais alto para computadores clássicos.
Os pesquisadores esperam que, no futuro, esta implementação do algoritmo de Grover pode ser ampliada para bancos de dados maiores. Conforme o tamanho do banco de dados aumenta, a vantagem quântica sobre os computadores clássicos fica ainda maior, que é onde as aplicações futuras serão beneficiadas.
"Seguindo em frente, planejamos continuar desenvolvendo sistemas com controle aprimorado sobre mais qubits, "Figgatt disse.
© 2018 Phys.org