Os cientistas descobrem mais de 600 novas órbitas periódicas do famoso problema dos três corpos
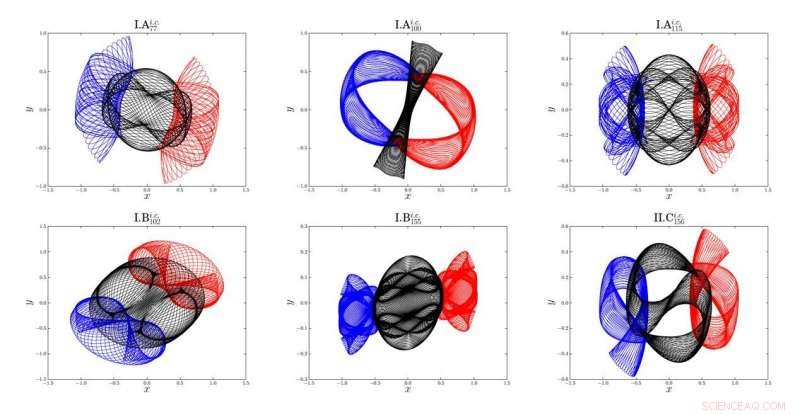 p Breve visão geral das seis famílias recém-descobertas de órbitas periódicas de três corpos. Linha azul:órbita do Corpo-1; linha vermelha:órbita do corpo-2; linha preta:órbita do corpo-3 Crédito:© Science China Press
p Breve visão geral das seis famílias recém-descobertas de órbitas periódicas de três corpos. Linha azul:órbita do Corpo-1; linha vermelha:órbita do corpo-2; linha preta:órbita do corpo-3 Crédito:© Science China Press
p O famoso problema dos três corpos remonta a Isaac Newton em 1680. Estudos sobre o problema dos três corpos levaram à descoberta da chamada dependência de sensibilidade da condição inicial (SDIC) de sistemas dinâmicos caóticos. Hoje, dinâmicas caóticas são amplamente consideradas como a terceira grande revolução científica da física no século 20, comparável à relatividade e à mecânica quântica. Assim, estudos sobre o problema dos três corpos têm um significado científico muito importante. p Em 1890, Poincaré determinou que as trajetórias dos sistemas de três corpos são comumente não periódicas, ou seja, não se repetindo. Isso pode explicar por que é tão difícil obter as órbitas periódicas de sistemas de três corpos. Nos 300 anos desde que o problema dos três corpos foi reconhecido pela primeira vez, apenas três famílias de órbitas periódicas foram encontradas. Em 2013, Suvakov e Dmitrasinovic [
Phys. Rev. Lett. 110, 114301 (2013)] fez uma descoberta, encontrar 13 novas órbitas periódicas distintas pertencentes a 11 novas famílias do problema planar newtoniano de três corpos com massa igual e momento angular zero. Agora, dois cientistas, XiaoMing Li e ShiJun Liao na Shanghai Jiaotong University, China, determinaram com sucesso 695 famílias de órbitas periódicas do mesmo sistema planar newtoniano de três corpos usando o supercomputador TH-2 em Guangzhou, China. Seus resultados foram publicados em
CIÊNCIA CHINA-Física Mecânica e Astronomia . Vídeos dessas órbitas estão disponíveis aqui.
p Essas 695 órbitas periódicas incluem a conhecida família em forma de oito encontrada por Moore em 1993, as 11 famílias encontradas por Suvakov e Dmitrasinovic em 2013, e mais de 600 novas famílias relatadas pela primeira vez. Os dois cientistas usaram a chamada simulação numérica limpa (CNS), uma nova estratégia numérica para simulações confiáveis de sistemas dinâmicos caóticos proposta pelo segundo autor em 2009, que é baseado em uma alta ordem de séries de Taylor e dados de precisão múltipla, além de uma verificação de convergência / confiabilidade. O CNS pode reduzir os erros de truncamento e arredondamento de forma tão eficaz que o ruído numérico é insignificante durante um intervalo de tempo longo o suficiente, assim, órbitas mais periódicas do sistema de três corpos podem ser obtidas.
p Conforme relatado por Montgomery em 1998, cada órbita periódica no espaço real do sistema de três corpos corresponde a uma curva fechada na chamada "esfera de forma, "que se caracteriza por sua topologia usando o chamado" elemento de grupo livre ". O período médio de uma órbita é igual ao período da órbita dividido pelo comprimento do elemento de grupo livre correspondente. Essas 695 famílias sugerem que o quadrado do período médio vezes o cubo da energia cinética e potencial total é aproximadamente igual a uma constante. A terceira lei de Kepler generalizada revela que o sistema de três corpos tem algo em comum que pode aprofundar a compreensão do sistema de três corpos.
p De acordo com os cientistas, a descoberta de mais de 600 novas órbitas periódicas deve-se principalmente ao avanço da informática e ao uso da nova estratégia de simulação numérica para sistemas dinâmicos caóticos, ou seja, o CNS. Deve-se enfatizar que mais 243 novas órbitas periódicas do sistema de três corpos são encontradas por meio do SNC. Em outras palavras, se algoritmos tradicionais com precisão dupla fossem usados, cerca de 40 por cento das novas órbitas periódicas seriam perdidas. Isso indica a novidade e originalidade do CNS, uma vez que quaisquer novos métodos devem oferecer algo novo.
