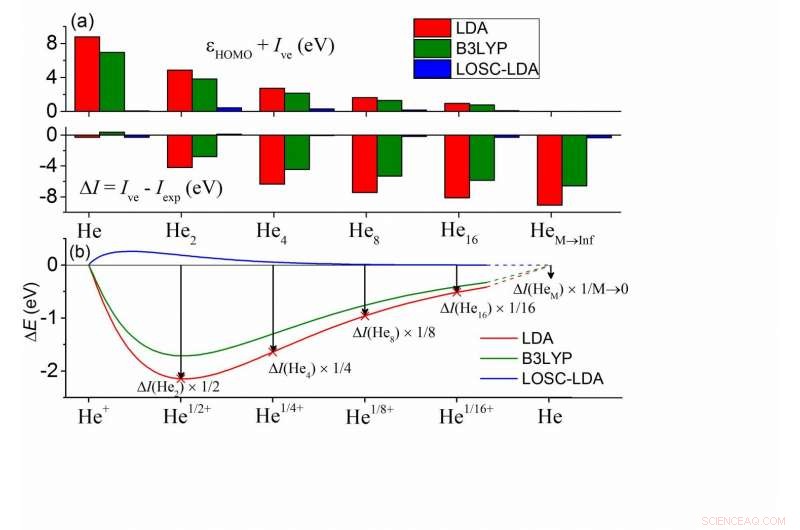
(a) Desvios entre o calculado? HOMO e -Ive e entre Ive e Iexp para uma série de clusters HeM. Em cada cluster, todos os átomos de He são quimicamente equivalentes. Os átomos vizinhos mais próximos são separados por 10Å, e o Iexp de HeM é bem aproximado por Iexp de um átomo de He. (b) Desvio de energia total calculado a partir da condição de linearidade de um átomo de He com carga fracionária em função da carga fracionária δ. Aqui ΔE (Heδ +) =E (Heδ +) - δE (He +) - (1-δ) E (He), e os valores de δ foram escalados na figura para uma comparação direta com (a). Crédito:© Science China Press
A teoria do funcional da densidade de Kohn-Sham é uma das teorias mais bem-sucedidas da química. É formalmente rigoroso; seu custo computacional relativamente baixo e precisão competitiva em sistemas de pequeno e médio porte o tornam um dos métodos mais populares em cálculos de estrutura eletrônica, e talvez a única escolha para modelar efeitos quânticos de elétrons em grandes sistemas químicos e biológicos. No entanto, o funcional exato não é explicitamente conhecido e as aproximações funcionais de densidade (DFAs) de última geração sofrem de erros sistemáticos. Um dos erros dominantes em DFAs é o erro de deslocalização, que é onipresente e se manifesta de várias maneiras. Este tem sido um problema aberto desafiador por décadas. Recentemente, Chen Li, Neil Qiang Su e Weitao Yang da Duke University e Xiao Zheng da University of Science and Technology da China desenvolveram uma nova estrutura de correção de escala orbital localizada (LOSC) que demonstra a eliminação sistemática do erro de deslocalização.
As principais consequências dos erros de deslocalização em DFAs podem ser categorizadas em dois aspectos:(1) Erro de energia orbital de Kohn-Sham (KS) e (2) erro de energia total. O erro de deslocalização leva a falhas importantes em aplicações práticas, como a subestimação não física de intervalos de banda, as distribuições de elétrons excessivamente deslocalizadas e as transferências de carga incorretas. Em relação a esses dois aspectos de erros, ambos se manifestam de maneira dependente do tamanho. Em particular, entre as energias orbitais KS, a energia orbital molecular ocupada mais alta (HOMO), εHOMO, é suposto concordar com o potencial de ionização vertical (negativo) (-Ive), conforme exigido pelo funcional exato. Além disso, o Ive calculado por DFAs deve concordar com o valor experimental, Iexp.
Para DFAs comumente usados, as duas condições não são satisfeitas. Conforme mostrado pelos cálculos do cluster de hélio na subfigura (a), a energia HOMO pela aproximação de densidade local (LDA) mostra um erro positivo em comparação com -Ive, enquanto Ive exibe um erro negativo, e os dois erros são exibidos de maneira dependente do tamanho, sugerindo que o erro de deslocalização de DFAs deve aparecer de uma forma ou de outra, ou ambos, enquanto a soma das magnitudes permanece inalterada. Além disso, isso prevalece em todos os tipos de DFAs, incluindo o funcional B3LYP mais popular, conforme mostrado em verde.
Para entender esses erros, os químicos podem mapeá-los nos erros de um átomo de He fracionado, conforme ilustrado na subfigura (b). As energias do sistema fracionário devem escalar linearmente com o número do elétron fracionário n (0? N <1) para o funcional exato. Mostrado na subfigura (b) está o desvio de energia da condição de linearidade para um único átomo de He, onde as energias fracionárias do sistema são subestimadas - isso define o erro de deslocalização. Além disso, o erro de carga fracionária em (b) tem correspondência 1-1 com o erro de energia total ΔI =Ive - Iexp. No limite de M vai ao infinito, pode-se deduzir que ΔI concorda com o erro de inclinação da curva E (N) no inteiro, que é exatamente o erro de energia HOMO de um único átomo de He. Portanto, todos os erros estão interligados. Assim, é possível eliminar o erro de deslocalização sistematicamente por meio de (1) remover os erros em (b) e (2) garantindo a remoção consistente do tamanho do erro em todos os sistemas.
No presente trabalho do LOSC, os autores inventaram novas variáveis locais, chamados orbitallets, que são orbitais localizados (LOs) que alcançam localidade em espaços espaciais e de energia. Através destes orbitallets, eles foram capazes de expressar a densidade de elétrons e a matriz de densidade KS na representação local, onde a matriz de ocupação local composta por números fracionários surge naturalmente. Portanto, essas variáveis locais são capazes de capturar informações fracionárias locais de forma precisa e completa no espaço orbital, e servem como blocos de construção perfeitos para o funcional LOSC. Além disso, reescrevendo os termos nos funcionais GSC e LSC em termos de fórmulas de correção de curvatura e fazendo analogia com o LOSC, eles introduziram uma matriz de curvatura local, cujos elementos são projetados como um funcional dos orbitallets, estar em correspondência direta com a matriz de ocupação local. Finalmente, a fórmula LOSC é escrita como uma expressão explícita e elegante sobre o funcional pai em termos dessas duas matrizes.
O LOSC atinge todos os recursos desejáveis. Na figura acima, os erros LOSC-LDA são essencialmente insignificantes, indicando a validade e consistência do tamanho da correção. Estes também foram validados pelas curvas de dissociação muito melhoradas de cátions moleculares diatômicos, variando de H2 +, He2 +, cátion dímero de água e cátion dímero de benzeno. O HOMO, Os erros de energia LUMO foram muito reduzidos e o bom desempenho é mantido conforme o tamanho do sistema aumenta. Isso foi demonstrado por testes em oligômeros de poliaceno e trans-poliacetileno. Além disso, o LOSC é capaz de recuperar a densidade de elétrons correta quando os DFAs pai o tornam qualitativamente errado, como mostrado pelo exemplo de um ânion cloro solvatado quando privado de um elétron.
O desempenho do LOSC, portanto, mostra a promessa de eliminar o erro de deslocalização sistematicamente dentro dos funcionais de densidade KS. É importante notar que, ao contrário do paradigma tradicional de projetar funcionais usando a densidade, os gradientes de densidade, a densidade de energia cinética, etc, a estrutura LOSC envolve ingredientes completamente novos, os orbitallets, que em si são funcionais implícitos da matriz de densidade KS, e demonstraram sua capacidade única de resolver problemas de longa data associados aos DFAs tradicionais. Isso reflete uma mudança de paradigma na concepção de funções, e amplia muito o caminho na exploração do exato funcional em seu próprio espaço de vida. Nesse sentido, LOSC inaugurou a tendência no desenvolvimento de uma nova geração de aproximações funcionais de densidade, promovendo a teoria do funcional da densidade a um novo nível de precisão.