
Este filme de sabão contido em uma haste de metal tem junções onde vários filmes de sabão se encontram. Em 2014, A professora Jenny Harrison, da UC Berkley, estendeu a solução para o problema do Plateau para dar conta de formatos de filme de sabão mais complicados como este. Crédito:Instituto de Ciência e Tecnologia de Okinawa
Freqüentemente usado para diversão infantil, bolhas de sabão são delicadas, filmes refletores de luz que normalmente duram apenas alguns segundos antes de estourar. Mas além de seu valor para entreter, bolhas de sabão são exemplos físicos do rico problema matemático das superfícies mínimas; eles assumem a forma da menor área de superfície possível, contendo um determinado volume. Pesquisadores da Universidade de Pós-Graduação do Instituto de Ciência e Tecnologia de Okinawa (OIST) descobriram recentemente a solução para um problema matemático - conhecido como o problema Kirchhoff-Plateau - que é simplesmente ilustrado por filmes de sabão que abrangem loops flexíveis.
"Nossa solução para o problema Kirchhoff-Plateau traz belos resultados matemáticos próximos ao que acontece no mundo físico, "diz o Dr. Giulio Giusteri, co-autor do artigo publicado recentemente no Journal of Nonlinear Science. Dr. Giusteri trabalhou com o professor Eliot Fried, que chefia a Unidade Matemática de Matéria Macia do OIST, e o Dr. Luca Lussardi da Università Cattolica del Sacro Cuore na Itália.
A pergunta respondida pela equipe é uma variante do "problema do Platô", um problema matemático secular, nomeado em homenagem a um físico belga do século 19, Joseph Plateau. Plateau levantou a hipótese de que, quando você mergulha uma estrutura de arame rígido em uma solução de sabão, a superfície da película de sabão formada na moldura representa uma área mínima matematicamente possível, não importa a forma da moldura.
A primeira solução satisfatória para o problema do Platô foi fornecida no século 20, pelo matemático americano Jesse Douglas, pelo qual foi premiado com a Medalha Fields em 1936. Mais recentemente, em 2014, A professora Jenny Harrison da UC Berkeley estendeu o trabalho de Douglas, fornecer uma prova válida sob hipóteses gerais que abrangem, por exemplo, situações em que as junções estão presentes onde vários filmes de sabão se encontram.
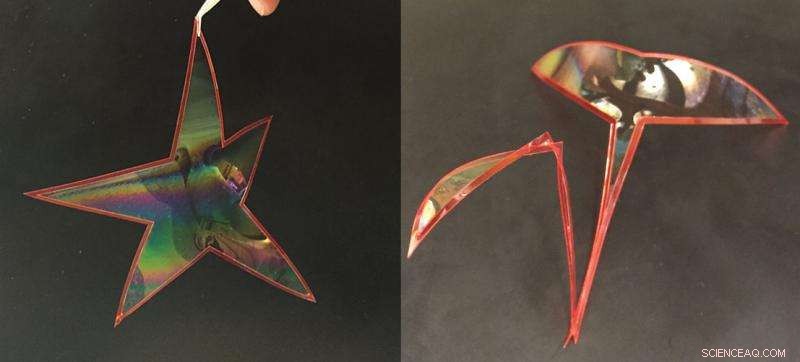
Filmes de sabão contidos em um loop flexível exercem uma força sobre o loop, fazendo com que ele mude de forma. Por exemplo, o mesmo laço pode ter a forma de uma estrela ou uma forma de cisne, dependendo da tensão superficial da película de sabão. Crédito:Instituto de Ciência e Tecnologia de Okinawa
Em contraste com o problema do Plateau, em que uma película de sabão abrange um quadro fixo, o problema de Kirchhoff-Plateau diz respeito às formas de equilíbrio de filmes de sabão que abrangem laços flexíveis, feito, por exemplo, de linha de pesca, que pode ser descrito usando a teoria das hastes de Kirchhoff - um modelo que fornece uma abordagem poderosa para estudar a estática e a dinâmica das hastes elásticas finas. A complicação é que uma alça flexível pode mudar de forma em resposta à força exercida pela película de sabão. Como tal, uma solução para o problema requer determinar não apenas a forma da película de sabão, mas também a forma do laço delimitador. Em contraste, a forma da fronteira no problema de Platô original é conhecida porque é feita de arame rígido que permanece fixo contra as forças relativamente fracas da película de sabão.
Uma complicação adicional associada ao problema Kirchhoff-Plateau é que, ao contrário do problema Plateau original, em que a fronteira é considerada unidimensional, uma haste de Kirchhoff é um objeto tridimensional. Embora os filamentos como a linha de pesca sejam finos, eles são ordens de magnitude mais espessos do que uma película de sabão em equilíbrio, o que significa que a área do filme de sabão pode mudar dependendo do ponto em que o filme entra em contato com o laço.
Os pesquisadores traduziram com sucesso todos esses efeitos físicos em termos matemáticos. Como o Prof. Fried explica:"Não importa o quão forte seja a competição entre a tensão superficial da película de sabão e a resposta elástica do loop, o sistema é sempre capaz de se ajustar para obter uma configuração de menor energia. "
A solução para o problema de Kirchhoff-Plateau não só contribui para a compreensão de formas matemáticas de minimização de energia, mas também pode ser aplicado a sistemas biológicos. Por exemplo, pode nos ajudar a entender como a forma de uma proteína determina como ela interage e se liga a uma superfície.
A equipe agora está trabalhando em simulações de computador que, com base neste modelo matemático, pode prever o comportamento de sistemas físicos.