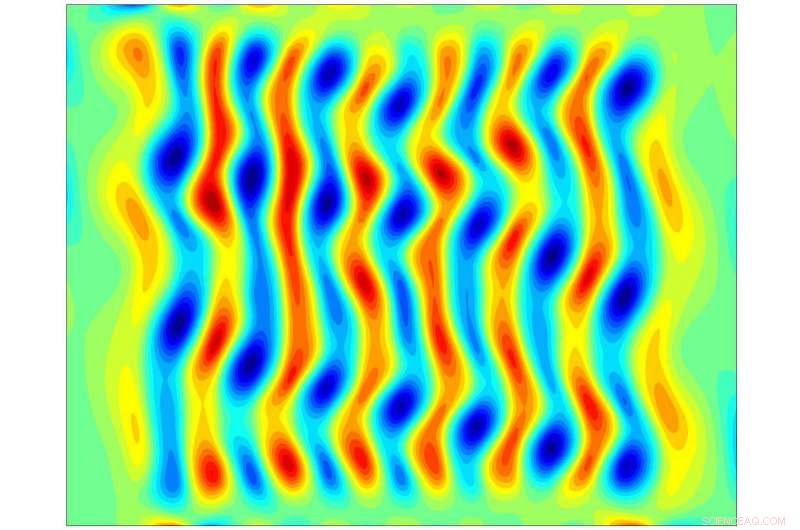
 p Um instantâneo analisado de um momento de fluxo turbulento, nesse caso, uma estrutura coerente exata (ECS). Crédito:Georgia Tech / Schatz / Grigoriev
p Um instantâneo analisado de um momento de fluxo turbulento, nesse caso, uma estrutura coerente exata (ECS). Crédito:Georgia Tech / Schatz / Grigoriev
p Um velho ditado diz que o bater da asa de uma borboleta no Brasil pode desencadear um tornado no Texas semanas depois. Embora a teoria do caos diga que é basicamente impossível calcular exatamente como isso pode acontecer, os cientistas fizeram avanços na aplicação da matemática para prever o fenômeno por trás disso, chamado turbulência. p O progresso recente dos físicos do Instituto de Tecnologia da Geórgia pode um dia ajudar a aprimorar as previsões do tempo e estender seu alcance, fazendo melhor uso das massas de dados meteorológicos e climáticos.
p A turbulência pode se curvar como um sopro de ar, giram além da curva de um rio ou agitam-se como um furacão, e embora seus arabescos possam parecer aleatórios, a turbulência estabelece padrões de assinatura que os físicos estão investigando. Eles desenvolveram um modelo matemático simples que os ajudou a mostrar como os fluxos turbulentos irão evoluir ao longo dos intervalos.
p E, em um novo experimento, eles verificaram suas previsões fisicamente em um fluxo turbulento bidimensional produzido em um laboratório.
p
Frase de efeito 'Efeito borboleta'
p A nova pesquisa da Georgia Tech condiz com as origens desse ditado.
p Ele foi cunhado há mais de 55 anos pelo professor de meteorologia do MIT Edward Lorenz depois que ele estabeleceu que pequenas forças influenciam o clima importante o suficiente para lançar previsões de longo alcance para um loop. O título de seu artigo, "Previsibilidade:o bater das asas de uma borboleta no Brasil desencadeou um tornado no Texas?" transformou-se na conhecida frase de efeito.
p Michael Schatz e Roman Grigoriev, professores da Escola de Física da Georgia Tech, junto com os pesquisadores graduados Balachandra Suri e Jeffrey Tithof, publicou seus resultados de pesquisa online no jornal
Cartas de revisão física na quarta-feira, 15 de março, 2017. A pesquisa foi financiada pela National Science Foundation.
p
Ordem no caos
p Por centenas de anos, enquanto os cientistas usaram a matemática para controlar a queda da maçã de Newton, fundamentar a Teoria da Relatividade e teorizar a existência do bóson de Higgs, a turbulência tem sido como sabão úmido nas mãos da matemática. Mas apesar de toda a sua indefinição, turbulência impressiona com visivelmente coerente, recorrente, formas reconhecíveis.
p Os redemoinhos de fluido se estabelecem rapidamente e depois mudam ou desaparecem, mas eles reaparecem persistentemente em locais diferentes, produzindo transiente e variável, ainda padrões de repetição.
p "As pessoas têm visto esses padrões em fluxos turbulentos há séculos, mas estamos encontrando maneiras de relacionar os padrões a equações matemáticas que descrevem fluxos de fluidos, "Grigoriev disse. Alguns padrões recorrentes, em particular, interesse Grigoriev e Schatz. Eles são chamados de estruturas coerentes exatas (ECSs).
p Eles fornecem aos físicos pontos de entrada convenientes para calcular previsões sobre o que a turbulência fará em seguida.
p
Instantâneos de fluxo turbulento
p Mas quais são essas estruturas coerentes exatas? Visualmente, em turbulência, eles podem aparecer como momentos fugazes quando os padrões param de mudar. E pode parecer que o fluxo está diminuindo temporariamente.
p Para o olho destreinado, um ECS não parece muito diferente do resto dos redemoinhos e cachos, mas pode-se aprender a identificá-los. "É exatamente assim que fazemos para encontrá-los, "Schatz disse." Assistimos à turbulência, continuamente tirando instantâneos. O fluxo está se movendo, movendo-se em torno de. Procuramos o instante em que ele fica mais lento, e escolhemos um instantâneo. "
p "Colocamos isso no modelo matemático, "Schatz disse, "e indica que estamos perto, e mostra como a matemática se parece nesse ponto. "Essa solução matemática descreve um ponto no fluxo turbulento que pode ser trabalhado para calcular uma previsão do que a turbulência fará a seguir.
p Para entender o que é uma estrutura coerente exata dinamicamente, precisamos dar um passo atrás de como a turbulência se parece visualmente com cachos e redemoinhos. Em vez de, vamos olhar para um fluxo turbulento como uma única entidade física, traduzindo-o em uma metáfora crua, um pêndulo oscilante - com algumas esquisitices marcantes.
O bater da asa de uma borboleta no Brasil pode desencadear um tornado no Texas? A teoria do caos diz que calcular a turbulência para encontrar a resposta é basicamente impossível. Mas os físicos da Georgia Tech estão fazendo progressos na aplicação da matemática à turbulência e podem predizê-la em intervalos. Crédito:Georgia Tech / Ben Brumfield p
Pêndulo em sua cabeça
p Isso vai ficar um pouco abstrato:primeiro, inverta o pêndulo.
p Em vez de retratar o ponto inferior da oscilação de um pêndulo normal, o equilíbrio, como um ponto estável em um balanço estável, agora, com o pêndulo de cabeça para baixo, o equilíbrio é o ponto mais alto. E é instável. Também, não oscila apenas em duas direções, mas em todas as direções.
p Os padrões confiáveis de um fluxo turbulento refletem dinâmicas que vão e vêm, mas em todos os tipos de variações.
p Conforme o pêndulo metafórico oscila em direção ao seu pico, chega a uma parada próxima, mas nunca completa. Em vez disso, ele cai para outro lado. Esse ponto de quase parada é análogo a uma estrutura coerente exata, mas existem mais algumas torções na metáfora.
p "Se mudarmos a dinâmica inicial um pouco, um pêndulo invertido pode oscilar além de seu equilíbrio instável no pico, ou pode parar e começar a se mover na direção oposta. Do mesmo jeito, o fluxo turbulento pode evoluir de várias maneiras diferentes depois de passar por um ECS, "Grigoriev disse.
p Múltiplas estruturas coerentes exatas com qualidades variadas surgem em um fluxo turbulento.
p
Estradas de turbulência para cidades ECS
p Que tudo pode parecer incomum por um motivo.
p "Usualmente, as pessoas gostam de olhar para coisas estáveis que são imutáveis, como pêndulo normal simétrico, "Schatz disse." Acontece que são realmente esses padrões instáveis que formam um alfabeto básico bruto que usamos para construir uma espécie de teoria preditiva. "
p Permanecendo com a dinâmica daquele pêndulo invertido flexível, agora imagine cada estrutura coerente exata como sendo uma cidade em um mapa. Existem caminhos que orientam o fluxo turbulento de "tráfego" em direção a, a partir de, e ao redor de cada cidade como estradas. "Este roteiro ao redor e entre as cidades não muda com o tempo, o que nos permite prever a evolução do fluxo, "Grigoriev disse.
p ECSs ocorrem regularmente, quase como um relógio, abrindo a possibilidade de refinar as previsões em intervalos regulares.
p Já se sabia da existência de estruturas exatas e coerentes, Schatz disse. "O que ninguém fez antes foi demonstrar em um experimento de laboratório como eles podem ser aproveitados para descrever a dinâmica, o comportamento evoluindo com o tempo, que é realmente o que você precisa para fazer previsões. "
p
Dados meteorológicos de mineração
p No século 19, equações matemáticas foram desenvolvidas para descrever o fluxo básico de fluidos. Aqueles que fizeram física do ensino médio podem se lembrar da Segunda Lei de Newton, que relaciona as forças, aceleração e massa. As equações de Navier-Stokes, usado neste estudo, aplique-o aos fluidos.
p A turbulência é difícil de descrever matematicamente porque seus redemoinhos contêm uma miríade de dimensões, com o fluxo em cada pequena região parecendo dançar em sua própria melodia. Mas existe uma ordem clara que surge ao se encontrar estruturas coerentes exatas.
p Para fazer suas previsões, A equipe de pesquisa de Schatz e Grigoriev desenvolveu uma maneira de conectar matematicamente essa alta dimensionalidade ao conceito de estrada muito mais simples.
p Eles quebraram o fluxo turbulento em regiões, cada um pequeno o suficiente para aplicar as equações, em seguida, usaram suas soluções para colocar precisamente os fluxos no roteiro.
p Hoje, o compêndio de dados sobre tempo e clima, a forma do fundo do oceano, dimensões da atmosfera, efeitos da gravidade, rotação, ou concentrações de minerais dissolvidos é impressionante e crescente.
p Métodos preditivos como os desta pesquisa oferecem caminhos para esses dados para extrair melhores previsões deles.
