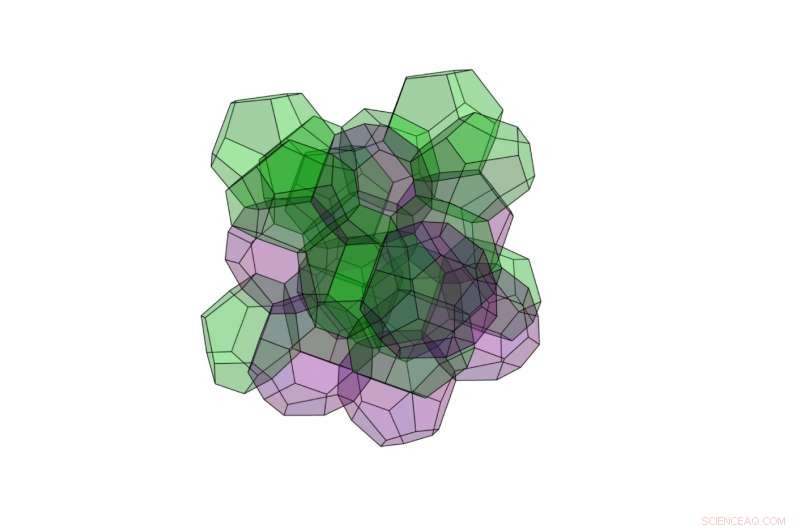
Uma das novas estruturas 3D tem a superfície mais baixa de qualquer estrutura de partição de espaço conhecida:é feita de 24 poliedros, alguns dos quais têm 12 faces e alguns dos quais 16 faces. Como os poliedros de 12 e 16 faces aqui têm volumes diferentes, a nova estrutura não atende ao requisito original de Kelvin para volumes iguais. Crédito:Opsomer e Vandewalle. © 2016 Publicação IOP
(Phys.org) —Os pesquisadores descobriram uma nova estrutura 3D que divide o espaço em 24 regiões, e mostraram que é a melhor solução para uma versão modificada de um problema de partição geométrica do espaço que desafiou os pesquisadores por mais de um século.
Em 1887, Lord Kelvin perguntou como o espaço poderia ser dividido em estruturas 3D de igual volume de uma forma que minimizasse a área total da superfície de cada estrutura. Deve ser possível compactar firmemente muitas dessas estruturas, sem lacunas entre elas - em outras palavras, devem ser estruturas que "preenchem o espaço". Cada estrutura pode assumir uma variedade de formas 3D complexas, ou "poliedros, "seja como um único poliedro ou uma combinação de vários poliedros menores de vários tipos. O desafio é descobrir quais tipos específicos de poliedros usar para minimizar a área da superfície externa de toda a estrutura.
A melhor solução de Kelvin para este problema foi um único poliedro chamado "tetrakaidecaedro, "que tem 14 faces:seis quadrados e oito hexágonos. Como esta é a forma obtida ao cortar os cantos de uma forma de diamante 3D, também pode ser considerado um octaedro truncado.
Embora a solução de Kelvin durasse mais de um século, em 1994, Denis Weaire e Robert Phelan, do Trinity College Dublin, usaram simulações numéricas para descobrir uma partição espacial mais adequada. A solução de Weaire e Phelan é feita de oito poliedros de dois tipos diferentes, embora ambos os tipos tenham o mesmo volume:seis do tetrakaidecaedro de Kelvin e dois dodecaedros (que tem 12 faces). Juntos, esses oito poliedros formam uma estrutura 3D que tem 0,3% menos área de superfície do que o tetrakaidecaedro único de Kelvin. A estrutura de Weaire-Phelan permaneceu como a solução ideal para o problema de Kelvin nos últimos 22 anos.
Agora no novo estudo, os físicos Eric Opsomer e Nicolas Vandewalle da Universidade de Liége, na Bélgica, desenvolveram um novo algoritmo para encontrar estruturas poliédricas compostas que preenchem o espaço com área de superfície mínima.
Usando o novo método, eles descobriram que uma nova estrutura 3D feita de 24 poliedros tem uma área de superfície ainda menor do que a estrutura de Weaire-Phelan. Os 24 poliedros são de dois tipos diferentes:alguns têm 12 faces e outros têm 16 faces. Ao contrário da estrutura Weaire-Phelan, em que os dois tipos diferentes de poliedros têm volumes iguais, os poliedros de 12 e 16 faces aqui têm volumes significativamente diferentes. Por esta razão, a nova estrutura não satisfaz o requisito original de Kelvin para volumes iguais.
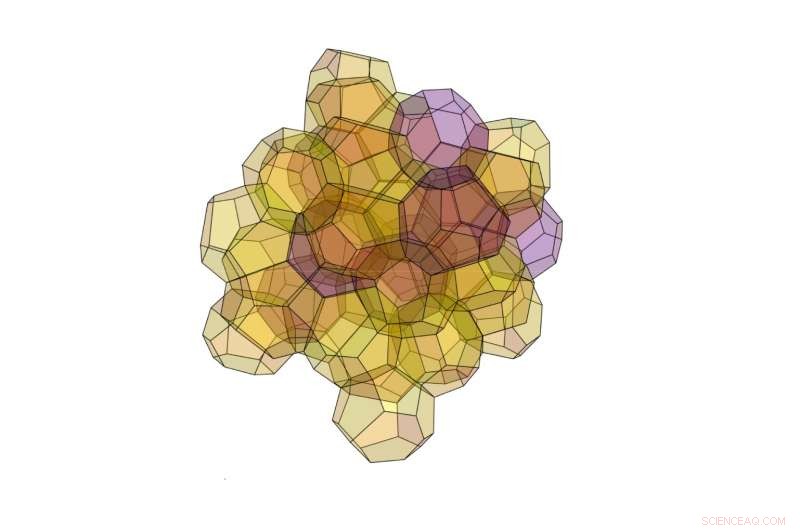
O novo algoritmo descobriu essa estrutura 3D composta por 40 poliedros de dois tipos diferentes. Crédito:Opsomer e Vandewalle. © 2016 Publicação IOP
"Infelizmente, não é uma 'solução verdadeira, 'uma vez que células de volume igual são um requisito para o problema Kelvin original, "Opsomer disse Phys.org . Apesar disso, a estrutura ainda é interessante por outras razões. "Esses resultados podem levar à descoberta de estruturas com implicações potenciais para a física dos materiais, pesquisa médica, e outras áreas, "Opsomer disse.
Como os pesquisadores explicaram, eles removeram intencionalmente a restrição de volumes iguais ao desenvolver seu método de pesquisa porque lhes permitiu projetar o algoritmo de uma nova maneira:em vez de minimizar diretamente a área de superfície de uma estrutura, eles maximizaram os isoperímetros médios dos poliedros (os perímetros compartilhados por todos os poliedros adjacentes). Embora essas duas abordagens sejam diferentes, eles são, em última análise, equivalentes.
Os pesquisadores usaram o novo algoritmo para explorar várias estruturas 3D feitas de dois a 64 poliedros. Começando com um número específico de pontos dispostos aleatoriamente no espaço 3D, o algoritmo começa a mover os pontos. Após cada iteração, o algoritmo calcula o novo isoperímetro médio, e com base no resultado mantém ou rejeita a nova configuração com uma certa probabilidade. Depois de milhões e às vezes bilhões de iterações, os pontos eventualmente formam os vértices de vários poliedros que, juntos, formam uma estrutura 3D com área de superfície muito baixa.
Como não há atualmente nenhuma maneira de provar qual é a estrutura de particionamento de espaço ideal (com ou sem células de volume igual), os pesquisadores planejam continuar pesquisando uma ampla variedade de estruturas de todos os tipos. Seu melhor palpite é que existem estruturas ainda mais ótimas, e eles planejam usar seu algoritmo para continuar sua exploração.
Os pesquisadores também esperam que o algoritmo possa gerar outras estruturas únicas. Uma estrutura particularmente interessante que eles descobriram aqui é uma estrutura de 40 poliedros que é mais ótima do que a estrutura de Kelvin, mas não tão boa quanto a estrutura de Weaire-Phelan. Esta estrutura altamente complexa também é incomum porque não pertence a uma categoria de estruturas chamadas estruturas de Frank-Kasper, que os pesquisadores têm tradicionalmente focado para o particionamento ideal do espaço. A descoberta sugere que outras estruturas ótimas também podem existir fora desta categoria.
Embora o problema de Kelvin não tenha sido proposto originalmente para atender a nenhuma necessidade prática, o particionamento de espaço ideal agora tem uma variedade de aplicativos. Na área médica, esses conceitos foram usados para criar projetos fortes, substituições leves de tecido ósseo. O particionamento ideal do espaço também inspirou a arquitetura, com um exemplo notável sendo o local de natação construído para os Jogos Olímpicos de Pequim em 2008. O edifício, que é chamado de Cubo d'Água, baseia-se na estrutura de Weaire-Phelan.
© 2016 Phys.org