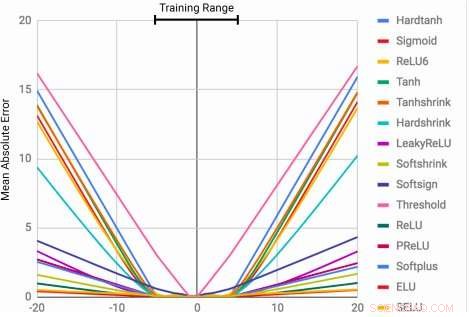
MLPs aprendem a função de identidade apenas para os valores de intervalo nos quais são treinados. O erro médio aumenta severamente, tanto abaixo quanto acima da faixa de números observada durante o treinamento. Crédito:Trask et al.
A capacidade de representar e manipular quantidades numéricas pode ser observada em muitas espécies, incluindo insetos, mamíferos e humanos. Isso sugere que o raciocínio quantitativo básico é um componente importante da inteligência, que tem várias vantagens evolutivas.
Esse recurso pode ser muito valioso em máquinas, permitindo a conclusão mais rápida e eficiente de tarefas que envolvem a manipulação de números. Ainda, até aqui, redes neurais treinadas para representar e manipular informações numéricas raramente foram capazes de generalizar bem fora da faixa de valores encontrados durante o processo de treinamento.
Uma equipe de pesquisadores do Google DeepMind desenvolveu recentemente uma nova arquitetura que aborda essa limitação, alcançar melhor generalização dentro e fora da faixa de valores numéricos em que a rede neural foi treinada. Seu estudo, que foi pré-publicado no arXiv, poderia informar o desenvolvimento de ferramentas de aprendizado de máquina mais avançadas para concluir tarefas de raciocínio quantitativo.
"Quando as arquiteturas neurais padrão são treinadas para contar até um número, eles muitas vezes lutam para contar para um maior, "Andrew Trask, pesquisador líder do projeto, disse Tech Xplore. "Exploramos essa limitação e descobrimos que ela se estende a outras funções aritméticas também, levando à nossa hipótese de que as redes neurais aprendem números semelhantes a como aprendem palavras, como um vocabulário finito. Isso os impede de extrapolar corretamente funções que requerem números (mais altos) anteriormente não vistos. Nosso objetivo era propor uma nova arquitetura que pudesse realizar uma melhor extrapolação. "

O Acumulador Neural (NAC) é uma transformação linear de suas entradas. A matriz de transformação é o produto elementar de tanh (Wˆ) e σ (Mˆ). A Unidade Lógica Aritmética Neural (NALU) usa dois NACs com pesos amarrados para permitir adição / subtração (célula roxa menor) e multiplicação / divisão (célula roxa maior), controlado por um portão (célula laranja). Crédito:Trask et al.
Os pesquisadores desenvolveram uma arquitetura que incentiva uma extrapolação de número mais sistemática, representando quantidades numéricas como ativações lineares que são manipuladas usando operadores aritméticos primitivos, que são controlados por portas aprendidas. Eles chamaram este novo módulo de unidade lógica aritmética neural (NALU), inspirado na unidade lógica aritmética em processadores tradicionais.
"Os números são geralmente codificados em redes neurais usando representações one-hot ou distribuídas, e funções sobre números são aprendidas dentro de uma série de camadas com ativações não lineares, "Trask explicou." Propomos que os números sejam armazenados como escalares, armazenar um único número em cada neurônio. Por exemplo, se você quiser armazenar o número 42, você deve apenas ter um neurônio contendo uma ativação de exatamente '42, 'em vez de uma série de 0-1 neurônios que o codificam. "
Os pesquisadores também mudaram a maneira como a rede neural aprende funções com base nesses números. Em vez de usar arquiteturas padrão, que pode aprender qualquer função, eles desenvolveram uma arquitetura que propaga um conjunto predefinido de funções que são vistas como potencialmente úteis (por exemplo, adição, multiplicação ou divisão), usando arquiteturas neurais que aprendem mecanismos de atenção sobre essas funções.
"Esses mecanismos de atenção então decidem quando e onde cada função potencialmente útil pode ser aplicada em vez de aprender essa função em si, "Trask disse." Este é um princípio geral para a criação de redes neurais profundas com um viés de aprendizagem desejável sobre funções numéricas. "

(acima) Quadros da tarefa de rastreamento de tempo do gridworld. O agente (cinza) deve se mover para o destino (vermelho) em um horário especificado. (abaixo) NAC melhora a capacidade de extrapolação aprendida por agentes A3C para a tarefa de datação. Crédito:Trask et al.
O teste revelou que as redes neurais aprimoradas com NALU podem aprender a realizar uma variedade de tarefas, como rastreamento de tempo, realizando funções aritméticas sobre imagens de números, traduzindo a linguagem numérica em escalares de valor real, execução de código de computador e contagem de objetos em imagens.
Em comparação com as arquiteturas convencionais, seu módulo obteve uma generalização significativamente melhor dentro e fora da faixa de valores numéricos com os quais foi apresentado durante o treinamento. Embora o NALU possa não ser a solução ideal para todas as tarefas, seu estudo fornece uma estratégia de design geral para a criação de modelos que funcionam bem em uma classe particular de funções.
"A noção de que uma rede neural profunda deve selecionar a partir de um conjunto predefinido de funções e aprender os mecanismos de atenção que regem onde eles são usados é uma ideia muito extensível, "Trask explicou." Neste trabalho, exploramos funções aritméticas simples (adição, subtração, multiplicação e divisão), mas estamos entusiasmados com o potencial de aprender mecanismos de atenção sobre funções muito mais poderosas no futuro, talvez trazendo os mesmos resultados de extrapolação que observamos para uma ampla variedade de campos. "
© 2018 Tech Xplore