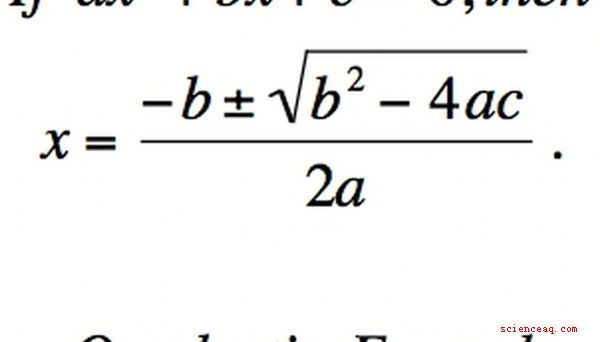
A fatoração de um polinômio se refere a encontrar polinômios de ordem inferior (o maior expoente é menor) que, multiplicados juntos, produzem o polinômio sendo fatorado. Por exemplo, x ^ 2 - 1 pode ser fatorado em x - 1 e x + 1. Quando esses fatores são multiplicados, o -1x e + 1x se cancelam, deixando x ^ 2 e 1.

Of Limited Power Review

Infelizmente, o factoring não é uma ferramenta poderosa, o que limita seu uso na vida cotidiana e nos campos técnicos. Os polinômios são fortemente manipulados no ensino fundamental para que possam ser fatorados. Na vida cotidiana, os polinômios não são tão amigáveis ​​e exigem ferramentas de análise mais sofisticadas. Um polinômio tão simples quanto x ^ 2 + 1 não é fatorável sem usar números complexos - isto é, números que incluem i = √ (-1). Polinômios de ordem tão baixos quanto 3 podem ser proibitivamente difíceis de fatorar. Por exemplo, x ^ 3 - y ^ 3 fatores para (x - y) (x ^ 2 + xy + y ^ 2), mas não são mais necessários sem recorrer a números complexos.

High School Science < Os polinômios de segunda ordem - por exemplo, x ^ 2 + 5x + 4 - são regularmente considerados nas aulas de álgebra, por volta do oitavo ou nono ano. O propósito de fatorar tais funções é então ser capaz de resolver equações de polinômios. Por exemplo, a solução para x ^ 2 + 5x + 4 = 0 são as raízes de x ^ 2 + 5x + 4, a saber, -1 e -4. Ser capaz de encontrar as raízes de tais polinômios é básico para resolver problemas em aulas de ciências nos seguintes 2 a 3 anos. Fórmulas de segunda ordem surgem regularmente em tais classes, por exemplo, em problemas de projétil e cálculos de equilíbrio ácido-base.

A fórmula quadrática

Em chegando com melhores ferramentas para substituir o factoring, você deve Lembre-se de que o objetivo do factoring está em primeiro lugar: resolver equações. A fórmula quadrática é uma maneira de contornar a dificuldade de fatorar alguns polinômios enquanto ainda serve ao propósito de resolver uma equação. Para equações de polinômios de segunda ordem (isto é, da forma ax ^ 2 + bx + c), a fórmula quadrática é usada para encontrar as raízes do polinômio e, portanto, a solução da equação. A fórmula quadrática é x = [-b +/- √ (b ^ 2 - 4ac)] /[2a], onde +/- significa "mais ou menos". Observe que não há necessidade de escrever (x - root1) (x - root2) = 0. Em vez de fatorar para resolver a equação, a solução da fórmula pode ser resolvida diretamente sem fatoração como uma etapa intermediária, embora o método seja baseado em factorization.

Isto não quer dizer que factoring é dispensável. Se os alunos aprendessem a equação quadrática de resolver equações de polinômios sem factoring de aprendizagem, a compreensão da equação quadrática seria reduzida.

Exemplos

Isso não quer dizer que a fatoração de polinômios nunca é feita fora de aulas de álgebra, física e química. As calculadoras financeiras portáteis executam um cálculo de juros diários usando uma fórmula que consiste na fatoração de pagamentos futuros com o componente de juros retirado (veja o diagrama). Em equações diferenciais (equações de taxas de mudança), a fatoração de polinômios de derivadas (taxas de mudança) é realizada para resolver o que é chamado de "equações homogêneas de ordem arbitrária". Outro exemplo está no cálculo introdutório, no método de frações parciais para facilitar a integração (solução para a área sob uma curva).

Soluções computacionais e o uso da aprendizagem de plano de fundo

Esses exemplos são claro, longe do cotidiano. E quando o factoring fica difícil, temos calculadoras e computadores para fazer o trabalho pesado. Em vez de esperar uma correspondência um-para-um entre cada tópico matemático ensinado e cálculos diários, observe a preparação que o tópico fornece para um estudo mais prático. O factoring deve ser apreciado pelo que é: um trampolim para aprender métodos de resolução de equações cada vez mais realistas.