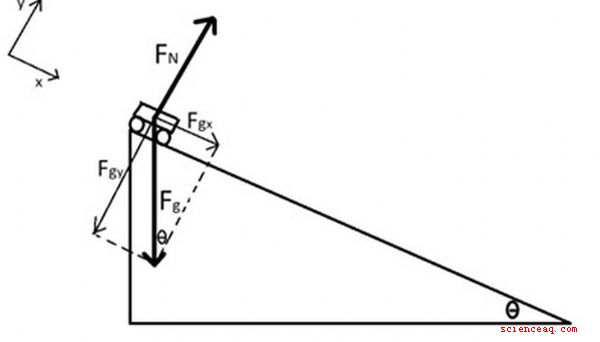
A força líquida
é a soma vetorial de todas as forças que atuam em um corpo. (Lembre-se de que uma força é um empurrão ou uma tração.) A unidade SI para força é o newton (N), onde 1 N \u003d 1 kgm /s ^{2.
\\ bold {F_ {net}} \u003d \\ bold {F_1 + F_2 + F_3 + ...}}

A primeira lei de Newton afirma que um objeto em movimento uniforme - o que significa que ele está em repouso ou se move com velocidade constante - continuará a fazê-lo, a menos que seja acionado por uma rede diferente de zero força. A segunda lei de Newton nos diz explicitamente como o movimento mudará como resultado dessa força líquida:
\\ bold {F_ {net}} \u003d m \\ bold {a}

A aceleração - mudança na velocidade ao longo do tempo - é diretamente proporcional à força líquida. Observe também que a aceleração e a força líquida são quantidades vetoriais que apontam na mesma direção.

TL; DR (muito longo; não leu)

Uma força líquida igual a zero NÃO necessariamente significa que o objeto está parado! Uma força líquida igual a zero também NÃO significa que não há forças agindo sobre um objeto, pois é possível que várias forças ajam de maneira a se anularem.
Diagramas de Corpo Livre

O primeiro passo para encontrar força líquida em qualquer objeto é desenhar um diagrama de corpo livre (FBD) mostrando todas as forças que atuam sobre esse objeto. Isso é feito representando cada vetor de força como uma flecha originária do centro do objeto e apontando na direção em que a força está agindo.

Por exemplo, suponha que um livro esteja sentado em uma mesa. As forças que agem sobre ele seriam a força da gravidade no livro, agindo para baixo, e a força normal da mesa no livro, agindo para cima. O diagrama de corpo livre desse cenário consistiria em duas setas de igual comprimento originárias do centro do livro, uma apontando para cima e a outra apontando para baixo.

(imagem 1)

Suponha o mesmo livro estava sendo empurrado para a direita com uma força de 5 N, enquanto uma força de atrito de 3 N se opunha ao movimento. Agora, o diagrama de corpo livre incluiria uma seta 5-N à direita e uma seta 3-N à esquerda.

(imagem 2)

Finalmente, suponha que o mesmo livro esteja uma inclinação, deslizando para baixo. Nesse cenário, as três forças são a força gravitacional do livro, que aponta diretamente para baixo; a força normal no livro, que aponta perpendicularmente à superfície; e a força de atrito, que aponta oposta à direção do movimento.

(imagem 3)
Cálculo da força líquida

Depois de desenhar o diagrama de corpo livre, você pode usar a adição de vetores para encontrar a força resultante atuando sobre o objeto. Consideraremos três casos ao explorarmos essa idéia:

Caso 1: Todas as forças estão na mesma linha.

Se todas as forças estiverem na mesma linha (apontando apenas para a esquerda e direita) , ou apenas para cima e para baixo, por exemplo), determinar a força resultante é tão simples quanto adicionar as magnitudes das forças na direção positiva e subtrair as magnitudes das forças na direção negativa. (Se duas forças são iguais e opostas, como é o caso do livro sobre a mesa, a força líquida \u003d 0)

Exemplo: Considere uma bola de 1 kg caindo devido à gravidade, experimentando uma resistência do ar força de 5 N. Existe uma força descendente devido à gravidade de 1 kg × 9,8 m /s 2 \u003d 9,8 N e uma força ascendente de 5 N. Se usarmos a convenção de que up é positivo, então a força líquida é 5 N - 9,8 N \u003d -4,8 N, indicando uma força líquida de 4,8 N na direção descendente.

(imagem 4)

Caso 2: Todas as forças estão perpendiculares eixos e adicione 0 ao longo de um eixo.

Nesse caso, devido às forças adicionando 0 em uma direção, precisamos focar apenas na direção perpendicular ao determinar a força líquida. (Embora o conhecimento de que as forças na primeira direção sejam adicionadas a 0 às vezes pode nos fornecer informações sobre as forças na direção perpendicular, como ao determinar forças de atrito em termos da magnitude normal da força.)

Exemplo: A O carro de brinquedo de 0,25 kg é empurrado pelo chão com uma força 3-N agindo para a direita. Uma força de atrito 2-N atua contra esse movimento. Observe que a gravidade também atua para baixo neste carro com uma força de 0,25 kg × 9,8 m /s 2 \u003d 2,45 N, e uma força normal atua para cima, também com 2,45 N. (Como sabemos disso? Como não há mudança de movimento na direção vertical à medida que o carro é empurrado pelo piso, a força resultante na direção vertical deve ser 0.)
Isso simplifica tudo o caso unidimensional, porque as únicas forças que não cancelam estão ao longo de uma direção. A força resultante no carro é então 3 N - 2 N \u003d 1 N para a direita.

(imagem 5)

Caso 3: Todas as forças não estão confinadas a uma linha e não estão em eixos perpendiculares.

Se soubermos em que direção estará a aceleração, escolheremos um sistema de coordenadas em que essa direção se encontra no eixo x positivo ou no eixo y positivo. A partir daí, dividimos cada vetor de força em componentes x e y. Como o movimento em uma direção é constante, a soma das forças nessa direção deve ser 0. As forças na outra direção são os únicos contribuidores da força resultante, e este caso foi reduzido para o Caso 2.

Se não soubermos em que direção a aceleração estará, podemos escolher qualquer sistema de coordenadas cartesianas, embora seja geralmente mais conveniente escolher um no qual uma ou mais das forças estejam sobre um eixo. Divida cada vetor de força em componentes x e y. Determine a força líquida na direção x
e a força líquida na direção y
separadamente. O resultado fornece as coordenadas x e y da força líquida.

Exemplo: Um carro de 0,25 kg rola sem atrito em uma inclinação de 30 graus devido à gravidade.

Usaremos um sistema de coordenadas alinhado com a rampa, como mostrado. O diagrama do corpo livre consiste na gravidade agindo diretamente para baixo e a força normal agindo perpendicular à superfície.

Devemos quebrar a força gravitacional nos componentes x e y, o que fornece:
F_ { gx} \u003d F_g \\ sin (\\ theta) \\\\ F_ {gy} \u003d F_g \\ cos (\\ theta)

Como o movimento na direção y
é constante, sabemos que a força resultante na y na direção deve ser 0:
F_N - F_ {gy} \u003d 0

(Nota: Esta equação nos permite determinar a magnitude da força normal.)

Na direção x, a única força é F _{gx
, portanto:
F_ {net} \u003d F_ {gx} \u003d F_g \\ sin (\\ theta) \u003d mg \\ sin (\\ theta) \u003d 0,25 \\ times9,8 \\ times \\ sin (30) \u003d 1,23 \\ text {N} Como encontrar aceleração da força líquida}

Depois de determinar seu vetor de força líquida, localize o a aceleração de um objeto é uma aplicação simples da segunda lei de Newton.
\\ bold {F_ {net}} \u003d m \\ bold {a} \\ implica \\ bold {a} \u003d \\ frac {\\ bold {F_ {net}} } {m}

No exemplo anterior do carro de 0,25 kg rolando pela rampa, a força líquida estava 1,23 N abaixo da rampa, portanto a aceleração seria:
\\ bold {a} \u003d \\ frac {\\ bold {F_ {net}}} {m} \u003d \\ frac {1,23} {0,25 } \u003d 4,92 \\ text {m /s} ^ 2 \\ text {descendo a rampa}