Novos modelos inspirados em kirigami preveem como os novos metamateriais se comportam
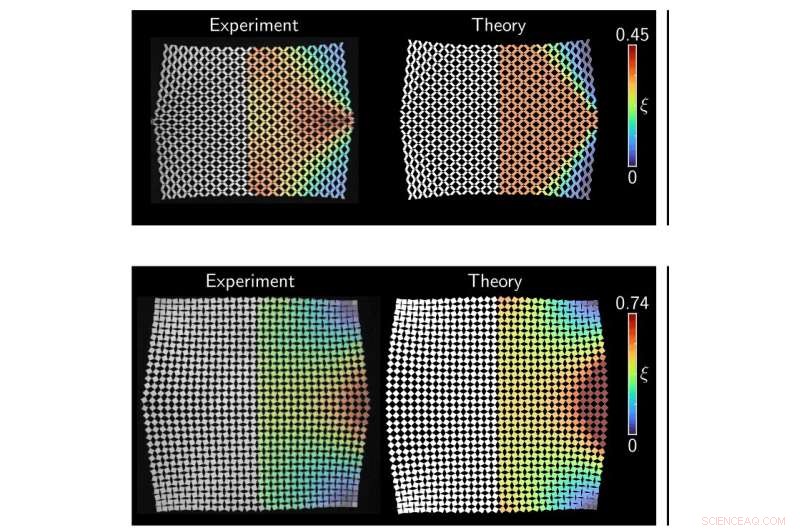
Dois padrões de células 16 × 16 após a deformação. A linha superior é não auxética (contrai quando puxada) e hiperbólica ou ondulada. A linha inferior é auxética (se expande quando puxada) e elíptica. Crédito:Paul Plucinsky
Um guindaste de papel tradicional é uma façanha de arte. Cada dobra no origami leva à transformação de uma única folha quadrada de papel em um pássaro, um dragão ou uma flor. O origami desencoraja colar, marcar ou cortar o papel, mas na arte do kirigami, cortes estrategicamente colocados podem transformar ainda mais a forma do papel, criando estruturas complexas a partir de simples fendas. Um exemplo bem conhecido disso é um livro pop-up, onde dependendo de como o papel plano é cortado, um conjunto diferente de formas – um coração, um sapo, um conjunto de arranha-céus – surgirá quando o livro for aberto.
Na fabricação, o kirigami está mudando o jogo do que é possível. Assim como com o papel, o corte a laser repetido de uma folha abre a possibilidade de transformações complexas de formas alimentadas pela abertura e fechamento de fendas. Devido à liberdade disponível no projeto de fendas, isso cria uma ampla escolha de geometrias que possuem propriedades altamente adaptáveis em comparação com materiais tradicionais. Em aplicações do mundo real, você pode ver esse material usado em robótica ou espaço, por exemplo, uma pele de cobra como material inspirado em kirigami que permite que um robô rasteje ou uma fuselagem em transformação. Mas antes que esses materiais possam ser adaptados para uso profissional, precisamos entender melhor como os materiais kirigami mudam de forma sob tensões e cargas típicas de engenharia. Embora as regras para blocos de construção simples sejam conhecidas, as regras para suas interações coletivas de mudança de forma permanecem em grande parte obscuras.
Em um artigo recente publicado em
Physical Review Letters , uma equipe interdisciplinar de pesquisadores da USC, da Universidade de Illinois em Chicago e da Stony Brook University derivou uma nova equação matemática para categorizar o comportamento de materiais inspirados em kirigami para prever melhor como eles se moverão quando empurrados ou puxados. A equipe inclui o professor assistente da USC Paul Plucinsky e o bolsista de pós-doutorado Yue Zheng; Stony Brook University professor assistente Paolo Celli e assistente de pesquisa de pós-graduação Imtiar Niloy; e o professor assistente da Universidade de Illinois-Chicago, Ian Tobasco.
Disse Plucinsky:"A geometria desses materiais é ajustada de forma um tanto arbitrária. Portanto, precisamos de regras sobre como você pode escolher as arquiteturas que vai fabricar. Uma vez que você tenha essas regras, você também precisa ser capaz de modelar o sistema para você faz alguma previsão razoável de como ele se deformará quando empurrado ou puxado."
Plucinsky diz que os modelos anteriores de comportamento do material não se aplicam aos materiais kirigami, pois não são sensíveis à geometria complicada de seus projetos. "Se você quiser usar esses materiais, primeiro precisa entender por que, quando você introduz esses padrões em cargas, eles produzem uma resposta muito não uniforme."
Quando um material é cortado, ele produz "células" ou espaços contidos que se repetem em um padrão, por exemplo, paralelogramos, disse Plucinsky. No caso de materiais kirigami, essas células podem ser categorizadas para se comportar de duas maneiras:como ondas ou decaindo ao longo de arcos elípticos, e isso depende apenas se o padrão comprime ou expande perpendicularmente à direção de tração. Uma equação matemática governa o comportamento geométrico de coisas como o fluxo de água, disse Plucinsky, mas para sólidos como esses, é mais difícil deduzir. Uma equação diferencial parcial (EPD) é o que Plucinsky e sua equipe conseguiram desenvolver e estabelecer como a primeira peça de um quebra-cabeça maior necessário para tornar os materiais de kirigami praticamente aplicáveis.
Um problema de modelagem No momento, Plucinsky diz que enquanto as pessoas estão ansiosas para usar materiais de kirigami para projetar dispositivos nas áreas de robótica leve, biomédica e até mesmo espaço de pesquisa, há um problema básico de modelagem que impede seu uso. Plucinsky disse que não se sabe muito sobre como os materiais kirigami funcionam sob condições básicas de carregamento. "Se você não tiver uma boa ferramenta para modelar os sistemas em questão, terá dificuldade em investigar o espaço de design e fazer previsões abrangentes sobre os padrões individuais", disse Plucinsky.
À luz disso, Plucinsky e sua equipe de pesquisa pensaram:'existe uma equação matemática simples que possa caracterizar esses materiais? ."
A chave para a equação foi perceber que as células kirigami, apesar de terem blocos de construção complicados, poderiam ser conceituadas como átomos em uma rede (um conjunto 2D repetido de átomos), como em um sólido cristalino convencional, onde as unidades são idênticas e repetidas. . A partir daí, foi simples derivar uma equação que conseguisse refletir as mudanças na estrutura física de tal material quando manipulado. A equação fornece informações sobre cenários do mundo real, por exemplo, como um objeto espacial baseado em kirigami pode reagir se uma rocha lunar pousasse nele.
Peças de design de quebra-cabeça Os padrões Kirigami, disse Plucinsky, são benéficos por muitas razões, uma das quais é que são independentes do material de várias maneiras. "Isso se assemelha muito à manufatura aditiva, onde agora eles podem basicamente entrar e, em várias escalas, criar padrões cuidadosamente projetados. O ponto é que o padrão importa, então se você projetar o padrão corretamente, a escolha do material que você usa não importa t tem que importar tanto."
Ver o sucesso do modelo matemático na previsão de materiais inspirados em kirigami abre as portas para usar essa modelagem para outros materiais, disse Plucinsky. "Estamos trabalhando com a ideia de que, se você tem algo com um padrão repetitivo, pode encontrar uma equação que o modele com precisão. A partir daí, podemos virar isso de cabeça para baixo para que, se você quiser projetar uma propriedade específica, pode dizer, 'oh, ele precisa apresentar um padrão do tipo x' e fazer engenharia reversa".
+ Explorar mais Origami, kirigami inspiram projetos de metamateriais mecânicos
