Usando geometria termodinâmica para otimizar motores térmicos microscópicos de tempo finito
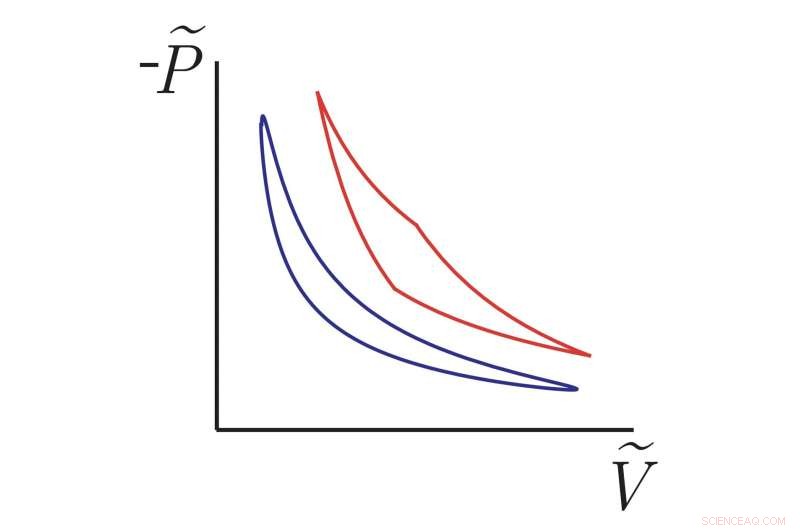
Ciclos termodinâmicos recém-descobertos (curva azul suave) aproximam-se de um novo limite geométrico de eficiência, superando outros motores fora de equilíbrio, como o ciclo de Carnot (curva vermelha) operando em tempo finito. Os eixos vertical e horizontal representam análogos de pressão e volume (negativos) para um motor microscópico consistindo de uma partícula presa a uma mola sendo golpeada por flutuações térmicas de seu ambiente. Estas são curvas teóricas baseadas em nossos resultados matemáticos, mas os experimentalistas desenvolveram recentemente métodos para medir a eficiência desses tipos de sistemas para que nossos resultados possam ser testados. Crédito:Frim &DeWeese.
A termodinâmica estocástica é uma área emergente da física destinada a melhor compreensão e interpretação de conceitos termodinâmicos longe do equilíbrio. Ao longo dos últimos anos, descobertas nesses campos revolucionaram a compreensão geral de diferentes processos termodinâmicos operando em tempo finito.
Adam Frim e Mike DeWeese, dois pesquisadores da Universidade da Califórnia, Berkeley (UC Berkeley), realizaram recentemente um estudo teórico explorando todo o espaço dos ciclos termodinâmicos com uma temperatura de banho em constante mudança. Seus resultados, apresentados em um artigo publicado em
Physical Review Letters , foram obtidos por métodos geométricos. A geometria termodinâmica é uma abordagem para entender a resposta de sistemas termodinâmicos por meio do estudo do espaço geométrico de controle.
“Por exemplo, para um gás em um pistão, uma coordenada neste espaço de controle pode corresponder ao volume experimentalmente controlado do gás e outra à temperatura”, disse DeWeese ao Phys.org. "Se um experimentalista girasse esses botões, isso traça alguma trajetória neste espaço termodinâmico. O que a geometria termodinâmica faz é atribuir a cada curva um 'comprimento termodinâmico' correspondente à energia dissipada mínima possível de um determinado caminho."
A geometria termodinâmica permite que os pesquisadores examinem questões de pesquisa interessantes, como a maneira ideal de manipular um determinado sistema nanoscópico, apagar um pouco de informação ou construir um motor térmico clássico ou quântico.
“Nosso principal objetivo neste artigo foi descobrir a maneira mais eficiente de operar um motor microscópico para que ele produza o trabalho mais útil para a quantidade de combustível que consome”, disse DeWeese ao Phys.org. "Enquanto a maioria dos estudos anteriores de geometria termodinâmica se concentrava em otimizar o controle de um sistema com determinadas configurações iniciais e finais, estávamos interessados em construir curvas fechadas ideais que pudessem funcionar como motores térmicos altamente eficientes".
As principais "regras" para entender como operar motores grandes com eficiência, como aqueles dentro de carros, quando operados lentamente, foram delineadas pela primeira vez há mais de um século, quando as leis da termodinâmica foram formuladas pela primeira vez. Em seu artigo, Frim e DeWeese estenderam essas teorias para que também pudessem ser aplicadas a motores microscópicos operando em tempo finito. Em contraste com grandes motores de operação lenta, esses motores não estão em equilíbrio térmico com o mundo externo e são fortemente afetados por flutuações térmicas no ambiente circundante.
"Em qualquer curso de termodinâmica de graduação, aprendemos que se você plotar pressão versus volume de um gás em um cilindro e considerar qualquer ciclo fechado que retorne ao mesmo ponto no gráfico, a área contida na curva fornece a quantidade de energia útil trabalho que você obtém de um ciclo deste motor térmico", disse DeWeese. "Isso pressupõe que você se move muito lentamente ao redor do ciclo, de modo que o gás no cilindro sempre permaneça próximo ao equilíbrio com o mundo exterior. Há uma analogia com este diagrama P-V para motores microscópicos, como uma pequena partícula presa a uma mola sendo atingido por flutuações térmicas de seu ambiente."
Quando eles traçaram ciclos no análogo de um diagrama P-V para um motor microscópico, Frim e DeWeese descobriram que uma função particular da área contida dentro da curva fechada ainda poderia ser pensada como a quantidade de trabalho útil fornecido por um ciclo do motor. . Além disso, verificou-se que o comprimento da curva fechada está relacionado com a quantidade de "trabalho útil" que foi perdido para a dissipação (ou seja, aquecer o ambiente sem ir para o funcionamento do motor).
"Nosso resultado é relativamente simples conceitualmente", explicou DeWeese. "Na geometria termodinâmica, comprimento é algo como dissipação. Então, pensamos:se você pegar um ciclo (um circuito fechado) com algum perímetro que tem comprimento fixo, o que representa a área dentro desse circuito? é algo como a saída de trabalho do ciclo, então, realmente, os ciclos ideais devem ter baixa dissipação e trabalho de alta saída, ou seja, um pequeno comprimento e uma grande área."
Explorando resultados geométricos clássicos, os pesquisadores conseguiram identificar protocolos ideais que estabelecem um limite na eficiência de todos os ciclos fechados. Suas descobertas podem contribuir significativamente para o projeto e desenvolvimento de motores térmicos microscópicos eficientes. O limite sobre a eficiência de ciclos termodinâmicos irreversíveis definido por esta equipe de pesquisadores é geral, portanto, suas implicações podem ir muito além dos motores microscópicos específicos considerados em seu artigo.
"Um dos nossos objetivos de longo prazo é desenvolver a teoria necessária para que os engenheiros projetem e construam motores muito pequenos e eficientes", disse DeWeese. "Esta pode vir a ser uma área importante da nanotecnologia. Também estamos fortemente motivados a entender a estrutura e função dos motores moleculares e outros tipos de 'máquinas' moleculares que vemos nas células de todas as criaturas e plantas."
Em seu trabalho, De Weese e Frim levantam a hipótese de que a evolução natural pode ter selecionado máquinas moleculares eficientes. Se esse fosse o caso, as regras que eles descobriram poderiam ser um primeiro passo para poder prever a estrutura e a função de máquinas moleculares que são onipresentes na biologia.
“Desigualdades isoperimétricas (ou seja, a interação de comprimentos e áreas de curvas fechadas) em abordagens geométricas da física podem ter inúmeras implicações no futuro”, acrescentou DeWeese. "Nosso limite matemático é mais realista do que os resultados anteriores que assumiram que o motor estava muito próximo do equilíbrio térmico com o ambiente (ou banho de calor) em todos os momentos, mas ainda assumimos que o sistema está sendo acionado lentamente (ou seja, os parâmetros de controle são alterados lentamente). Estamos agora interessados em estender nossos resultados além deste regime para incluir sistemas mais distantes do equilíbrio."
+ Explorar mais 'motores térmicos' miniaturizados podem alimentar máquinas em nanoescala do futuro
© 2022 Science X Network
